Random mandalas deconstruction in R, Python, and Mathematica

Posted on March 1, 2022 by Anton Antonov Antonov

Today (2022-02-28) I gave a presentation Greater Boston useR Meetup titled “Random mandalas deconstruction with R, Python, and Mathematica”. (Link to the video recording.)

Here is the abstract:

In this presentation we discuss the application of different dimension reduction algorithms over collections of random mandalas. We discuss and compare the derived image bases and show how those bases explain the underlying collection structure. The presented techniques and insights (1) are applicable to any collection of images, and (2) can be included in larger, more complicated machine learning workflows. The former is demonstrated with a handwritten digits recognition
application; the latter with the generation of random Bethlehem stars. The (parallel) walk-through of the core demonstration is in all three programming languages: Mathematica, Python, and R.

Here is the related RStudio project: “RandomMandalasDeconstruction”.

Here is a link to the R-computations notebook converted to HTML: “LSA methods comparison in R”.

The Mathematica notebooks are placed in project’s folder “notebooks-WL”.

See the work plan status in the org-mode file “Random-mandalas-deconstruction-presentation-work-plan.org”.

Here is the mind-map for the presentation:

The comparison workflow implemented in the notebooks of this project is summarized in the following flow chart:

References

Time series search engines over COVID-19 data

Posted on January 27, 2021 by Anton Antonov Antonov

Introduction

In this article we proclaim the preparation and availability of interactive interfaces to two Time Series Search Engines (TSSEs) over COVID-19 data. One TSSE is based on Apple Mobility Trends data, [APPL1]; the other on The New York Times COVID-19 data, [NYT1].

Here are links to interactive interfaces of the TSSEs hosted (and publicly available) at shinyapps.io by RStudio:

Motivation: The primary motivation for making the TSSEs and their interactive interfaces is to use them as exploratory tools. Combined with relevant data analysis (e.g. [AA1, AA2]) the TSSEs should help to form better intuition and feel of the spread of COVID-19 and related data aggregation, public reactions, and government polices.

The rest of the article is structured as follows:

Brief descriptions the overall process, the data
Brief descriptions the search engines structure and implementation
Discussions of a few search examples and their (possible) interpretations

The overall process

For both search engines the overall process has the same steps:

Ingest the data
Do basic (and advanced) data analysis
Make (and publish) reports detailing the data ingestion and transformation steps
Enhance the data with transformed versions of it or with additional related data
Make a Time Series Sparse Matrix Recommender (TSSMR)
Make a Time Series Search Engine Interactive Interface (TSSEII)
Make the interactive interface easily accessible over the World Wide Web

Here is a flow chart that corresponds to the steps listed above:

Data

The Apple data

The Apple Mobility Trends data is taken from Apple’s site, see [APPL1]. The data ingestion, basic data analysis, time series seasonality demonstration, (graph) clusterings are given in [AA1]. (Here is a link to the corresponding R-notebook .)

The weather data was taken using the Mathematica function WeatherData, [WRI1].

(It was too much work to get the weather data using some of the well known weather data R packages.)

The New York Times data

The New York Times COVID-19 data is taken from GitHub, see [NYT1]. The data ingestion, basic data analysis, and visualizations are given in [AA2]. (Here is a link to the corresponding R-notebook .)

The search engines

The following sub-sections have screenshots of the TSSE interactive interfaces.

I did experiment with combining the data of the two engines, but did not turn out to be particularly useful. It seems that is more interesting and useful to enhance the Apple data engine with temperature data, and to enhance The New Your Times engine with the (consecutive) differences of the time series.

Structure

The interactive interfaces have three panels:

Nearest Neighbors
- Gives the time series nearest neighbors for the time series of selected entity.
- Has interactive controls for entity selection and filtering.
Trend Finding
- Gives the time series that adhere to a specified named trend.
- Has interactive controls for trend curves selection and entity filtering.
Notes
- Gives references and data objects summary.

Implementation

Both TSSEs are implemented using the R packages “SparseMatrixRecommender”, [AAp1], and “SparseMatrixRecommenderInterfaces”, [AAp2].

The package “SparseMatrixRecommender” provides functions to create and use Sparse Matrix Recommender (SMR) objects. Both TSSEs use underlying SMR objects.

The package “SparseMatrixRecommenderInterfaces” provides functions to generate the server and client functions for the Shiny framework by RStudio.

As it was mentioned above, both TSSEs are published at shinyapps.io. The corresponding source codes can be found in [AAr1].

Apple Mobility Trends Reports Search Engine

The Apple data TSSE has four types of time series (“entities”). The first three are normalized volumes of Apple maps requests while driving, transit transport use, and walking. (See [AA1] for more details.) The fourth is daily mean temperature at different geo-locations.

Here are screenshots of the panels “Nearest Neighbors” and “Trend Finding” (at interface launch):

The New York Times COVID-19 Data Search Engine

The New York Times TSSE has four types of time series (aggregated) cases and deaths, and their corresponding time series differences.

Here are screenshots of the panels “Nearest Neighbors” and “Trend Finding” (at interface launch):

Examples

In this section we discuss in some detail several examples of using each of the TSSEs.

Apple data search engine examples

Here are a few observations from [AA1]:

The COVID-19 lockdowns are clearly reflected in the time series.
The time series from the Apple Mobility Trends data shows strong weekly seasonality. Roughly speaking, people go to places they are not familiar with on Fridays and Saturdays. Other work week days people are more familiar with their trips. Since much lesser number of requests are made on Sundays, we can conjecture that many people stay at home or visit very familiar locations.

Here are a few assumptions:

Where people frequently go (work, school, groceries shopping, etc.) they do not need directions that much.
People request directions when they have more free time and will for “leisure trips.”
During vacations people are more likely to be in places they are less familiar with.
People are more likely to take leisure trips when the weather is good. (Warm, not raining, etc.)

Nice, France vs Florida, USA

Consider the results of the Nearest Neighbors panel for Nice, France.

Since French tend to go on vacation in July and August ([SS1, INSEE1]) we can see that driving, transit, and walking in Nice have pronounced peaks during that time:

Of course, we also observe the lockdown period in that geographical area.

Compare those time series with the time series from driving in Florida, USA:

We can see that people in Florida, USA have driving patterns unrelated to the typical weather seasons and vacation periods.

(Further TSSE queries show that there is a negative correlation with the temperature in south Florida and the volumes of Apple Maps directions requests.)

Italy and Balkan countries driving

We can see that according to the data people who have access to both iPhones and cars in Italy and the Balkan countries Bulgaria, Greece, and Romania have similar directions requests patterns:

(The similarities can be explained with at least a few “obvious” facts, but we are going to restrain ourselves.)

The New York Times data search engine examples

In Broward county, Florida, USA and Cook county, Illinois, USA we can see two waves of infections in the difference time series:

References

Data

[APPL1] Apple Inc., Mobility Trends Reports, (2020), apple.com.

[NYT1] The New York Times, Coronavirus (Covid-19) Data in the United States, (2020), GitHub.

[WRI1] Wolfram Research (2008), WeatherData, Wolfram Language function.

Articles

[AA1] Anton Antonov, “Apple mobility trends data visualization (for COVID-19)”, (2020), SystemModeling at GitHub/antononcube.

[AA2] Anton Antonov, “NY Times COVID-19 data visualization”, (2020), SystemModeling at GitHub/antononcube.

[INSEE1] Institut national de la statistique et des études économiques, “En 2010, les salariés ont pris en moyenne six semaines de congé”, (2012).

[SS1] Sam Schechner and Lee Harris, “What Happens When All of France Takes Vacation? 438 Miles of Traffic”, (2019), The Wall Street Journal

Packages, repositories

[AAp1] Anton Antonov, Sparse Matrix Recommender framework functions, (2019), R-packages at GitHub/antononcube.

[AAp2] Anton Antonov, Sparse Matrix Recommender framework interface functions, (2019), R-packages at GitHub/antononcube.

[AAr1] Anton Antonov, Coronavirus propagation dynamics, (2020), SystemModeling at GitHub/antononcube.

A monad for Epidemiologic Compartmental Modeling Workflows

Posted on January 2, 2021 by Anton Antonov Antonov

Version 0.8

Introduction

In this document we describe the design and demonstrate the implementation of a (software programming) monad, [Wk1], for Epidemiology Compartmental Modeling (ECM) workflows specification and execution. The design and implementation are done with Mathematica / Wolfram Language (WL). A very similar implementation is also done in R.

Monad’s name is “ECMMon”, which stands for “Epidemiology Compartmental Modeling Monad”, and its monadic implementation is based on the State monad package “StateMonadCodeGenerator.m”, [AAp1, AA1], ECMMon is implemented in the package [AAp8], which relies on the packages [AAp3-AAp6]. The original ECM workflow discussed in [AA5] was implemented in [AAp7]. An R implementation of ECMMon is provided by the package [AAr2].

The goal of the monad design is to make the specification of ECM workflows (relatively) easy and straightforward by following a certain main scenario and specifying variations over that scenario.

We use real-life COVID-19 data, The New York Times COVID-19 data, see [NYT1, AA5].

The monadic programming design is used as a Software Design Pattern. The ECMMon monad can be also seen as a Domain Specific Language (DSL) for the specification and programming of epidemiological compartmental modeling workflows.

Here is an example of using the ECMMon monad over a compartmental model with two types of infected populations:

The table above is produced with the package “MonadicTracing.m”, [AAp2, AA1], and some of the explanations below also utilize that package.

As it was mentioned above the monad ECMMon can be seen as a DSL. Because of this the monad pipelines made with ECMMon are sometimes called “specifications”.

Contents description

The document has the following structure.

The sections “Package load” and “Data load” obtain the needed code and data.
- (Needed and put upfront from the “Reproducible research” point of view.)
The section “Design consideration” provide motivation and design decisions rationale.
The section “Single site models” give brief descriptions of certain “seed” models that can be used in the monad.
The section “Single-site model workflow demo”, “Multi-site workflow demo” give demonstrations of how to utilize the ECMMon monad .
- Using concrete practical scenarios and “real life” data.
The section “Batch simulation and calibration process” gives methodological preparation for the content of the next two sections.
The section “Batch simulation workflow” and “Calibration workflow” describe how to do most important monad workflows after the model is developed.
The section “Future plans” outlines future directions of development.
- (The most interesting and important one is the “conversational agent” direction.)

Remark: One can read only the sections “Introduction”, “Design consideration”, “Single-site models”, and “Batch simulation and calibration process”. That set of sections provide a fairly good, programming language agnostic exposition of the substance and novel ideas of this document.

Package load

In this section we load packages used in this notebook:

Import["https://raw.githubusercontent.com/antononcube/SystemModeling/master/Projects/Coronavirus-propagation-dynamics/WL/MonadicEpidemiologyCompartmentalModeling.m"]; Import["https://raw.githubusercontent.com/antononcube/SystemModeling/master/Projects/Coronavirus-propagation-dynamics/WL/MultiSiteModelSimulation.m"] Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicTracing.m"] Import["https://raw.githubusercontent.com/antononcube/ConversationalAgents/master/Packages/WL/ExternalParsersHookup.m"]

Remark: The import commands above would trigger some other package imports.

Data load

In this section we ingest data using the “umbrella function” MultiSiteModelReadData from [AAp5]:

Read data

AbsoluteTiming[   aData = MultiSiteModelReadData[];   ]  (*{38.8635, Null}*)

Data summaries

ResourceFunction["RecordsSummary"] /@ aData

Transform data

Here we transform the population related data in a form convenient for specifying the simulations with it:

aPopulations = Association@Map[{#Lon, #Lat} -> #Population &, Normal[aData["CountyRecords"]]]; aInfected = Association@Map[{#Lon, #Lat} -> #Cases &, Normal[aData["CasesAndDeaths"]]]; aDead = Association@Map[{#Lon, #Lat} -> #Deaths &, Normal[aData["CasesAndDeaths"]]];

Geo-visualizations

Using the built-in function GeoHistogram we summarize the USA county populations, and COViD-19 infection cases and deaths:

Row@MapThread[GeoHistogram[KeyMap[Reverse, #1], Quantity[140, "Miles"], PlotLabel -> #2, PlotTheme -> "Scientific", PlotLegends -> Automatic, ImageSize -> Medium] &, {{aPopulations, aInfected, aDead}, {"Populations", "Infected", "Dead"}}]

(Note that in the plots above we have to reverse the keys of the given population associations.)

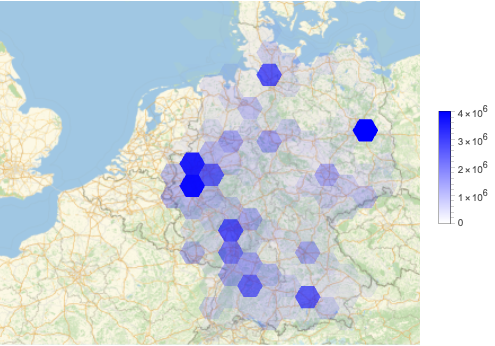
Using the function HextileHistogram from [AAp7 ] here we visualize USA county populations over a hexagonal grid with cell radius 2 degrees ((\approx 140) miles (\approx 222) kilometers):

HextileHistogram[aPopulations, 2, PlotRange -> All, PlotLegends -> Automatic, ImageSize -> Large]

In this notebook we prefer using HextileHistogram because it represents the simulation data in geometrically more faithful way.

Design considerations

The big picture

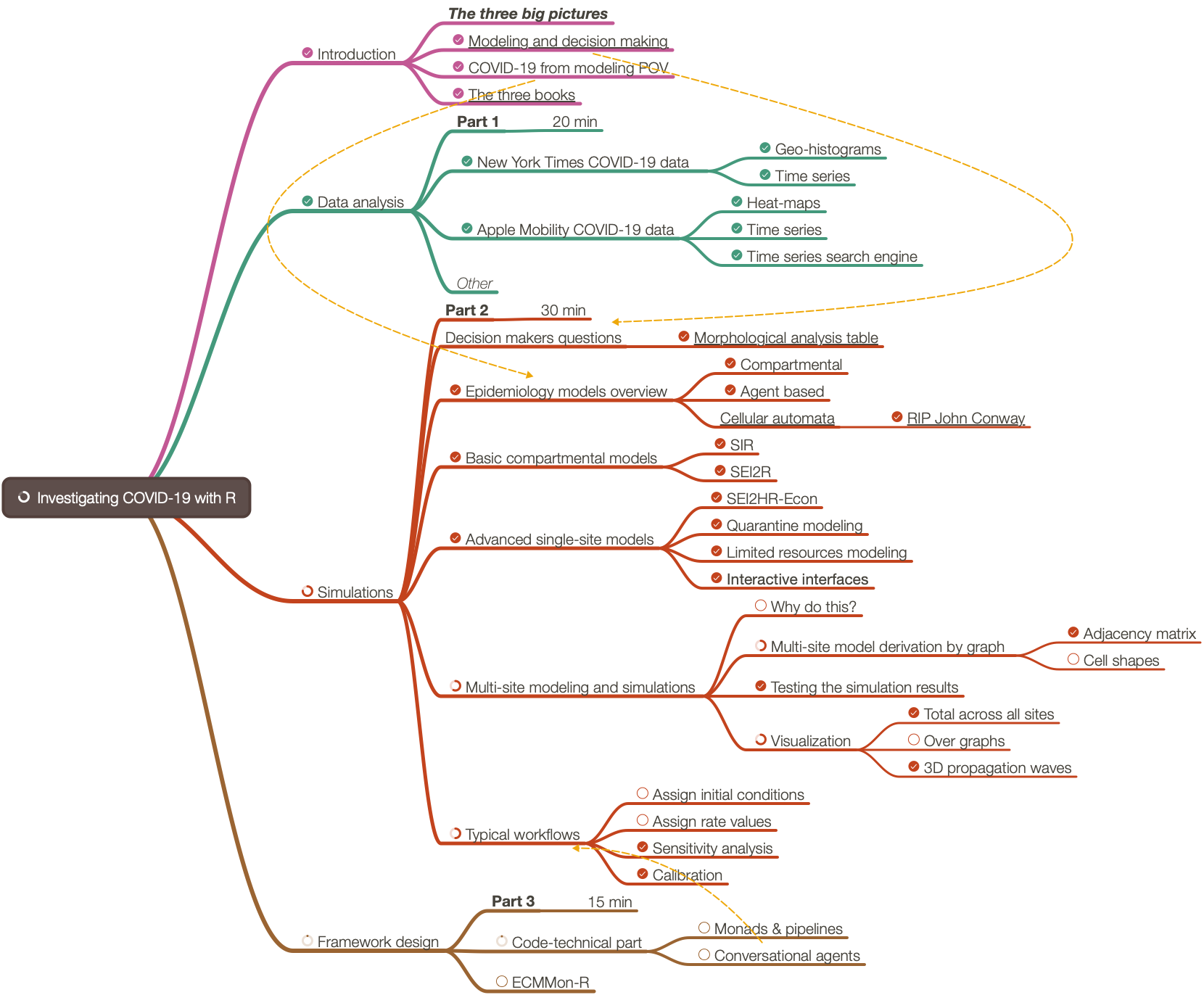
The main purpose of the designed epidemic compartmental modeling framework (i.e. software monad) is to have the ability to do multiple, systematic simulations for different scenario play-outs over large scale geographical regions. The target end-users are decision makers at government level and researchers of pandemic or other large scale epidemic effects.

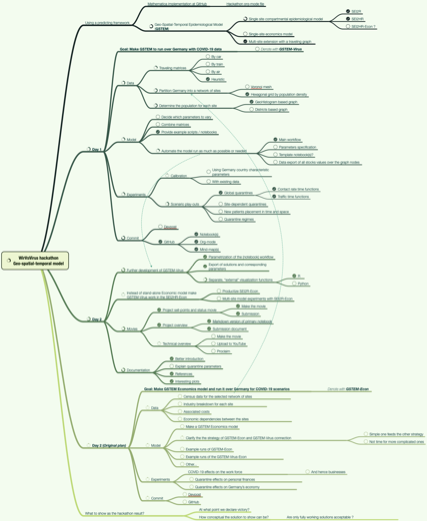
Here is a diagram that shows the envisioned big picture workflow:

Large-scale modeling

The standard classical compartmental epidemiology models are not adequate over large geographical areas, like, countries. We design a software framework – the monad ECMMon – that allows large scale simulations using a simple principle workflow:

Develop a single-site model for relatively densely populated geographical area for which the assumptions of the classical models (approximately) hold.
Extend the single-site model into a large-scale multi-site model using statistically derived traveling patterns; see [AA4].
Supply the multi-site model with appropriately prepared data.
Run multiple simulations to see large scale implications of different policies.
Calibrate the model to concrete observed (or faked) data. Go to 4.

Flow chart

The following flow chart visualizes the possible workflows the software monad ECMMon:

Two models in the monad

An ECMMon object can have one or two models. One of the models is a “seed”, single-site model from [AAp1], which, if desired, is scaled into a multi-site model, [AA3, AAp2].
Workflows with only the single-site model are supported.
- Say, workflows for doing sensitivity analysis, [AA6, BC1].
Scaling of a single-site model into multi-site is supported and facilitated.
Workflows for the multi-site model include preliminary model scaling steps and simulation steps.
After the single-site model is scaled the monad functions use the multi-site model.
The workflows should be easy to specify and read.

Single-site model workflow

Make a single-site model.
Assign stocks initial conditions.
Assign rates values.
Simulate.
Plot results.
Go to 2.

Multi-site model workflow

Make a single-site model.
Assign initial conditions and rates.
Scale the single-site model into a multi-site model.
1. The single-site assigned rates become “global” when the single-site model is scaled.
2. The scaling is based on assumptions for traveling patterns of the populations.
3. There are few alternatives for that scaling:
  1. Using locations geo-coordinates
  2. Using regular grids covering a certain area based on in-habited locations geo-coordinates
  3. Using traveling patterns contingency matrices
  4. Using “artificial” patterns of certain regular types for qualitative analysis purposes
Enhance the multi-site traveling patterns matrix and re-scale the single site model.
1. We might want to combine traveling patterns by ground transportation with traveling patterns by airplanes.
2. For quarantine scenarios this might a less important capability of the monad.
  1. Hence, this an optional step.
Assign stocks initial conditions for each of the sites in multi-scale model.
Assign rates for each of the sites.
Simulate.
Plot global simulation results.
Plot simulation results for focus sites.

Single-site models

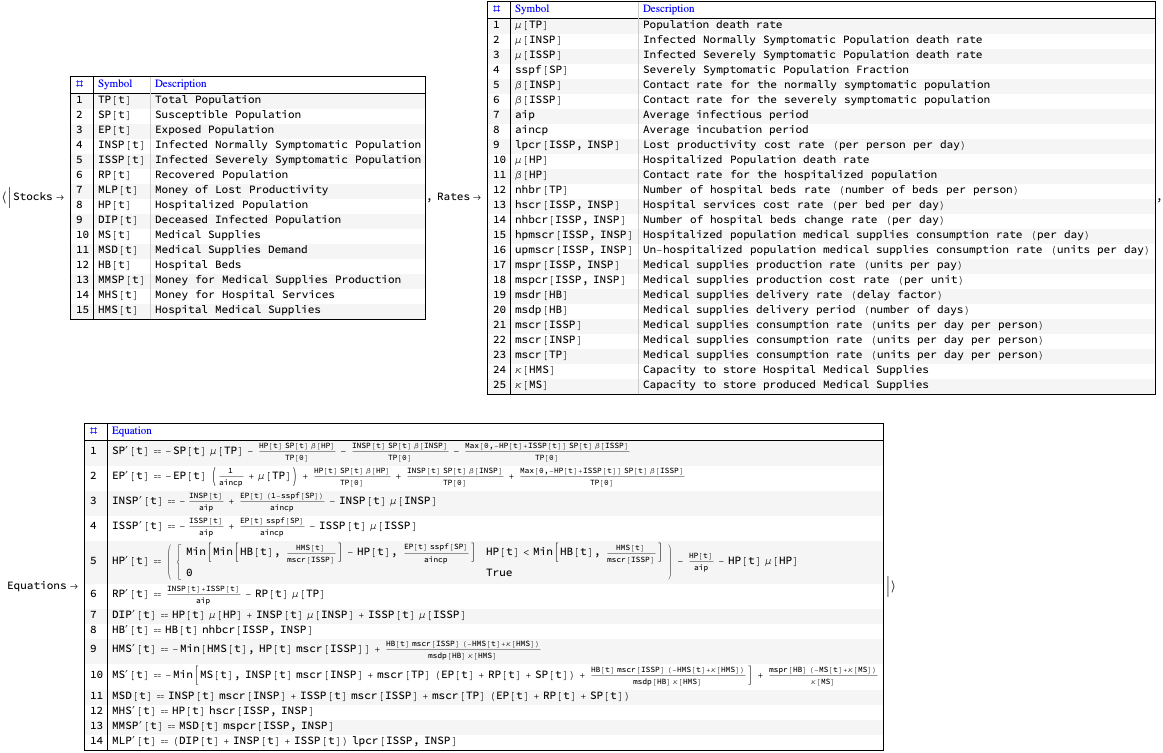
We have a collection of single-site models that have different properties and different modeling goals, [AAp3, AA7, AA8]. Here is as diagram of a single-site model that includes hospital beds and medical supplies as limitation resources, [AA7]:

SEI2HR model

In this sub-section we briefly describe the model SEI2HR, which is used in the examples below.

Remark: SEI2HR stands for “Susceptible, Exposed, Infected Two, Hospitalized, Recovered” (populations).

Detailed description of the SEI2HR model is given in [AA7].

Verbal description

We start with one infected (normally symptomatic) person, the rest of the people are susceptible. The infected people meet other people directly or get in contact with them indirectly. (Say, susceptible people touch things touched by infected.) For each susceptible person there is a probability to get the decease. The decease has an incubation period: before becoming infected the susceptible are (merely) exposed. The infected recover after a certain average infection period or die. A certain fraction of the infected become severely symptomatic. If there are enough hospital beds the severely symptomatic infected are hospitalized. The hospitalized severely infected have different death rate than the non-hospitalized ones. The number of hospital beds might change: hospitals are extended, new hospitals are build, or there are not enough medical personnel or supplies. The deaths from infection are tracked (accumulated.) Money for hospital services and money from lost productivity are tracked (accumulated.)

The equations below give mathematical interpretation of the model description above.

Equations

Here are the equations of one the epidemiology compartmental models, SEI2HR, [AA7], implemented in [AAp3]:

ModelGridTableForm[SEI2HRModel[t], "Tooltips" -> False]["Equations"] /. {eq_Equal :> TraditionalForm[eq]}

The equations for Susceptible, Exposed, Infected, Recovered populations of SEI2R are “standard” and explanations about them are found in [WK2, HH1]. For SEI2HR those equations change because of the stocks Hospitalized Population and Hospital Beds.

The equations time unit is one day. The time horizon is one year. In this document we consider COVID-19, [Wk2, AA1], hence we do not consider births.

Single-site model workflow demo

In this section we demonstrate some of the sensitivity analysis discussed in [AA6, BC1].

Make a single-site model, SEI2HR:

model1 = SEI2HRModel[t, "InitialConditions" -> True, "RateRules" -> True, "TotalPopulationRepresentation" -> "AlgebraicEquation"];

Make an association with “default” parameters:

aDefaultPars = <|     aip -> 26,      aincp -> 5,      \[Beta][ISSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],      \[Beta][INSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],      qsd -> 60,      ql -> 21,      qcrf -> 0.25,      \[Beta][HP] -> 0.01,      \[Mu][ISSP] -> 0.035/aip,      \[Mu][INSP] -> 0.01/aip,      nhbr[TP] -> 3/1000,      lpcr[ISSP, INSP] -> 1,      hscr[ISSP, INSP] -> 1     |>;

Execute the workflow multiple times with different quarantine starts:

qlVar = 56; lsRes =   Map[    ECMMonUnit[]⟹      ECMMonSetSingleSiteModel[model1]⟹      ECMMonAssignRateRules[Join[aDefaultPars, <|qsd -> #, ql -> qlVar|>]]⟹      ECMMonSimulate[365]⟹      ECMMonPlotSolutions[{"Infected Severely Symptomatic Population"}, 240,         "Together" -> True, "Derivatives" -> False,         PlotRange -> {0, 12000}, ImageSize -> 250,         Epilog -> {Orange, Dashed, Line[{{#1, 0}, {#1, 12000}}], Line[{{#1 + qlVar, 0}, {#1 + qlVar, 12000}}]},         PlotLabel -> Row[{"Quarantine start:", Spacer[5], #1, ",", Spacer[5], "end:", Spacer[5], #1 + qlVar}],         "Echo" -> False]⟹      ECMMonTakeValue &, Range[25, 100, 5]];

Plot the simulation solutions for “Infected Severely Symptomatic Population”:

Multicolumn[#[[1, 1]] & /@ lsRes, 4]

Both theoretical and computational details of the workflow above are given [AA7, AA8].

Multi-site workflow demo

In this section we demonstrate the multi-site model workflow using COVID-19 data for USA, [WRI2, NYT1].

Here a “seed”, single-site model is created:

model1 = SEI2HRModel[t, "InitialConditions" -> True, "RateRules" -> True, "TotalPopulationRepresentation" -> "AlgebraicEquation"];

Here we specify a multi-site model workflow (the monadic steps are separated and described with purple print-outs):

ecmObj =     ECMMonUnit[]⟹     ECMMonSetSingleSiteModel[model1]⟹     ECMMonAssignRateRules[      <|       aip -> 26,        aincp -> 5,        \[Beta][ISSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],        \[Beta][INSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],        qsd -> 0,        ql -> 56,        qcrf -> 0.25,        \[Beta][HP] -> 0.01,        \[Mu][ISSP] -> 0.035/aip,        \[Mu][INSP] -> 0.01/aip,        nhbr[TP] -> 3/1000,        lpcr[ISSP, INSP] -> 1,        hscr[ISSP, INSP] -> 1       |>      ]⟹     ECMMonEcho[Style["Show the single-site model tabulated form:", Bold, Purple]]⟹     ECMMonEchoFunctionContext[Magnify[ModelGridTableForm[#singleSiteModel], 1] &]⟹     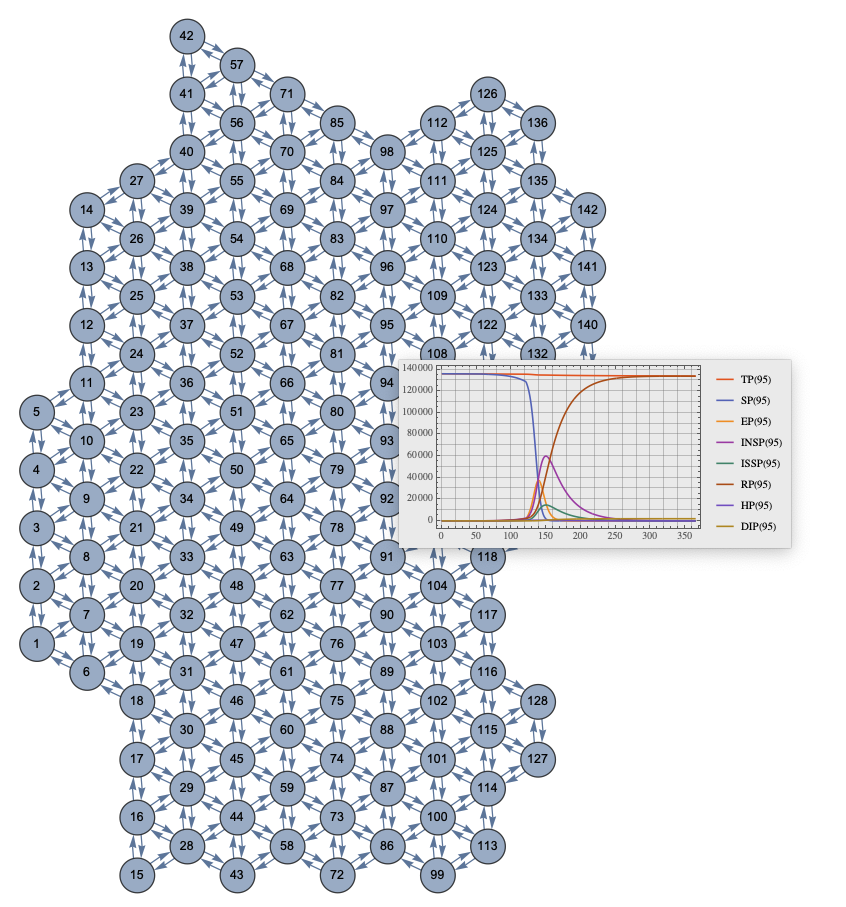ECMMonMakePolygonGrid[Keys[aPopulations], 1.5, "BinningFunction" -> Automatic]⟹     ECMMonEcho[Style["Show the grid based on population coordinates:", Bold, Purple]]⟹     ECMMonPlotGrid["CellIDs" -> True, ImageSize -> Large]⟹     ECMMonExtendByGrid[aPopulations, 0.12]⟹     ECMMonAssignInitialConditions[aPopulations, "Total Population", "Default" -> 0]⟹     ECMMonAssignInitialConditions[DeriveSusceptiblePopulation[aPopulations, aInfected, aDead], "Susceptible Population", "Default" -> 0]⟹     ECMMonAssignInitialConditions[<||>, "Exposed Population", "Default" -> 0]⟹     ECMMonAssignInitialConditions[aInfected, "Infected Normally Symptomatic Population", "Default" -> 0]⟹     ECMMonAssignInitialConditions[<||>, "Infected Severely Symptomatic Population", "Default" -> 0]⟹     ECMMonEcho[Style["Show total populations initial conditions data:", Bold, Purple]]⟹     ECMMonPlotGridHistogram[aPopulations, ImageSize -> Large, PlotLabel -> "Total populations"]⟹     ECMMonEcho[Style["Show infected and deceased initial conditions data:", Bold,Purple]]⟹     ECMMonPlotGridHistogram[aInfected, ColorFunction -> ColorData["RoseColors"], "ShowDataPoints" -> False, ImageSize -> Large, PlotLabel -> "Infected"]⟹     ECMMonPlotGridHistogram[aDead, ColorFunction -> ColorData["RoseColors"], "ShowDataPoints" -> False, ImageSize -> Large, PlotLabel -> "Deceased"]⟹     ECMMonEcho[Style["Simulate:", Bold, Purple]]⟹     ECMMonSimulate[365]⟹     ECMMonEcho[Style["Show global population simulation results:", Bold, Purple]]⟹     ECMMonPlotSolutions[__ ~~ "Population", 365]⟹     ECMMonEcho[Style["Show site simulation results for Miami and New York areas:", Bold, Purple]]⟹     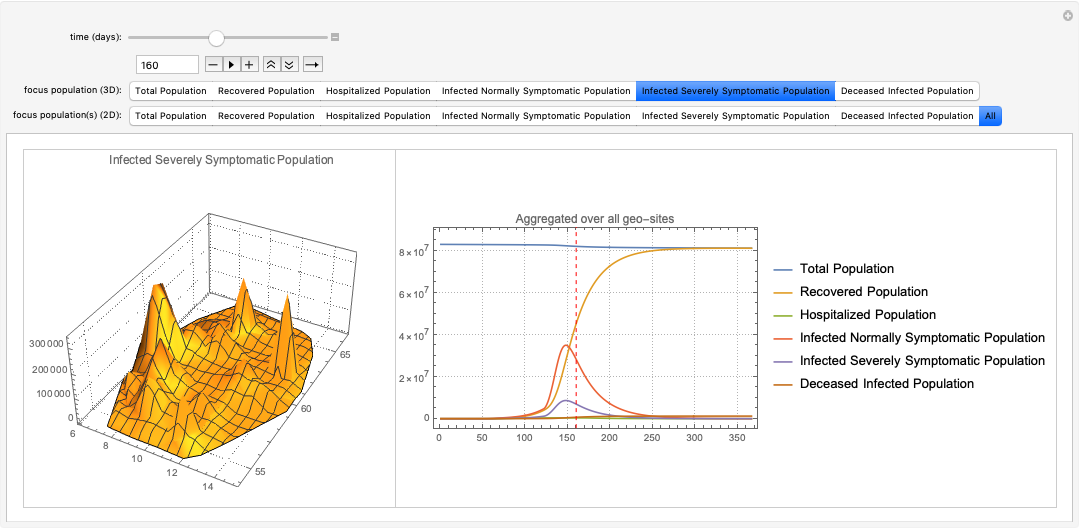ECMMonPlotSiteSolutions[{160, 174}, __ ~~ "Population", 365]⟹     ECMMonEcho[Style["Show deceased and hospitalzed populations results for Miami and New York areas:", Bold, Purple]]⟹     ECMMonPlotSiteSolutions[{160, 174}, {"Deceased Infected Population", "Hospitalized Population","Hospital Beds"}, 300, "FocusTime" -> 120];

Theoretical and computational details about the multi-site workflow can be found in [AA4, AA5].

Batch simulations and calibration processes

In this section we describe the in general terms the processes of model batch simulations and model calibration. The next two sections give more details of the corresponding software design and workflows.

Definitions

Batch simulation: If given a SD model (M), the set (P) of parameters of (M), and a set (B) of sets of values (P), (B\text{:=}\left{V_i\right}), then the set of multiple runs of (M) over (B) are called batch simulation.

Calibration: If given a model (M), the set (P) of parameters of (M), and a set of (k) time series (T\text{:=}\left{T_i\right}_{i=1}^k) that correspond to the set of stocks (S\text{:=}\left{S_i\right}_{i=1}^k) of (M) then the process of finding concrete the values (V) for (P) that make the stocks (S) to closely resemble the time series (T) according to some metric is called calibration of (M) over the targets (T).

Roles

There are three types of people dealing with the models:
- Modeler, who develops and implements the model and prepares it for calibration.
- Calibrator, who calibrates the model with different data for different parameters.
- Stakeholder, who requires different features of the model and outcomes from different scenario play-outs.
There are two main calibration scenarios:
- Modeler and Calibrator are the same person
- Modeler and Calibrator are different persons

Process

Model development and calibration is most likely going to be an iterative process.

For concreteness let us assume that the model has matured development-wise and batch simulation and model calibration is done in a (more) formal way.

Here are the steps of a well defined process between the modeling activity players described above:

Stakeholder requires certain scenarios to be investigated.
Modeler prepares the model for those scenarios.
Stakeholder and Modeler formulate a calibration request.
Calibrator uses the specifications from the calibration request to:
1. Calibrate the model
2. Derive model outcomes results
3. Provide model qualitative results
4. Provide model sensitivity analysis results
Modeler (and maybe Stakeholder) review the results and decides should more calibration be done.
1. I.e. go to 3.
Modeler does batch simulations with the calibrated model for the investigation scenarios.
Modeler and Stakeholder prepare report with the results.

See the documents [AA9, AA10] have questionnaires that further clarify the details of interaction between the modelers and calibrators.

Batch simulation vs calibration

In order to clarify the similarities and differences between batch simulation and calibration we list the following observations:

Each batch simulation or model calibration is done either for model development purposes or for scenario play-out studies.
Batch simulation is used for qualitative studies of the model. For example, doing sensitivity analysis; see [BC1, AA7, AA8].
Before starting the calibration we might want to study the “landscape” of the search space of the calibration parameters using batch simulations.
Batch simulation is also done after model calibration in order to evaluate different scenarios,
For some models with large computational complexity batch simulation – together with some evaluation metric – can be used instead of model calibration.

Batch simulations workflow

In this section we describe the specification and execution of model batch simulations.

Batch simulations can be time consuming, hence it is good idea to

In the rest of the section we go through the following steps:

Make a model object
Batch simulate over a few combinations of parameters and show:
1. Plots of the simulation results for all populations
2. Plots of the simulation results for a particular population
Batch simulate over the Cartesian (outer) product of values lists of a selected pair of parameters and show the corresponding plots of all simulations

Model (object) for batch simulations

Here we make a new ECMMon object:

ecmObj2 =   ECMMonUnit[]⟹    ECMMonSetSingleSiteModel[model1]⟹    ECMMonAssignRateRules[aDefaultPars];

Direct specification of combinations of parameters

All populations

Here we simulate the model in the object of different parameter combinations given in a list of associations:

res1 =   ecmObj2⟹    ECMMonBatchSimulate[___ ~~ "Population", {<|qsd -> 60, ql -> 28|>, <|qsd -> 55, ql -> 28|>, <|qsd -> 75, ql -> 21, \[Beta][ISSP] -> 0|>}, 240]⟹    ECMMonTakeValue;

Remark: The stocks in the results are only stocks that are populations – that is specified with the string expression pattern ___~~”Population”.

Here is the shape of the result:

Short /@ res1

Here are the corresponding plots:

ListLinePlot[#, PlotTheme -> "Detailed", ImageSize -> Medium, PlotRange -> All] & /@ res1

Focus population

We might be interested in the batch simulations results for only one, focus populations. Here is an example:

res2 =     ecmObj2⟹     ECMMonBatchSimulate["Infected Normally Symptomatic Population", {<|qsd -> 60, ql -> 28|>, <|qsd -> 55, ql -> 28|>, <|qsd -> 75, ql -> 21, \[Beta][ISSP] -> 0|>}, 240]⟹     ECMMonTakeValue;

Here is the shape of the result:

Short /@ res2

Here are the corresponding plots:

Multicolumn[  KeyValueMap[   ListLinePlot[#2, PlotLabel -> #1, PlotTheme -> "Detailed",      Epilog -> {Directive[Orange, Dashed],        Line[{Scaled[{0, -1}, {#1[qsd], 0}], Scaled[{0, 1}, {#1[qsd], 0}]}],        Line[{Scaled[{0, -1}, {#1[qsd] + #1[ql], 0}], Scaled[{0, 1}, {#1[qsd] + #1[ql], 0}]}]},      ImageSize -> Medium] &, res2]]

Outer product of parameters

Instead of specifying an the combinations of parameters directly we can specify the values taken by each parameter using an association in which the keys are parameters and the values are list of values:

res3 =     ecmObj2⟹     ECMMonBatchSimulate[__ ~~ "Population", <|qsd -> {60, 55, 75}, ql -> {28, 21}|>, 240]⟹     ECMMonTakeValue;

Here is the shallow form of the results

Short /@ res3

Here are the corresponding plots:

Multicolumn[  KeyValueMap[   ListLinePlot[#2, PlotLabel -> #1, PlotTheme -> "Detailed",      Epilog -> {Directive[Gray, Dashed],        Line[{Scaled[{0, -1}, {#1[qsd], 0}], Scaled[{0, 1}, {#1[qsd], 0}]}],        Line[{Scaled[{0, -1}, {#1[qsd] + #1[ql], 0}], Scaled[{0, 1}, {#1[qsd] + #1[ql], 0}]}]},      ImageSize -> Medium] &, res3]]

Calibration workflow

In this section we go through the computation steps of the calibration of single-site SEI2HR model.

Remark: We use real data in this section, but the presented calibration results and outcome plots are for illustration purposes only. A rigorous study with discussion of the related assumptions and conclusions is beyond the scope of this notebook/document.

Calibration steps

Here are the steps performed in the rest of the sub-sections of this section:

Ingest data for infected cases, deaths due to disease, etc.
Choose a model to calibrate.
Make the calibration targets – those a vectors corresponding to time series over regular grids.
1. Consider using all of the data in order to evaluate model’s applicability.
2. Consider using fractions of the data in order to evaluate model’s ability to predict the future or reconstruct data gaps.
Choose calibration parameters and corresponding ranges for their values.
If more than one target choose the relative weight (or importance) of the targets.
Calibrate the model.
Evaluate the fitting between the simulation results and data.
1. Using statistics and plots.
Make conclusions. If insufficiently good results are obtained go to 2 or 4.

Remark: When doing calibration epidemiological models a team of people it is better certain to follow (rigorously) well defined procedures. See the documents:

Remark: We plan to prepare have several notebooks dedicated to calibration of both single-site and multi-site models.

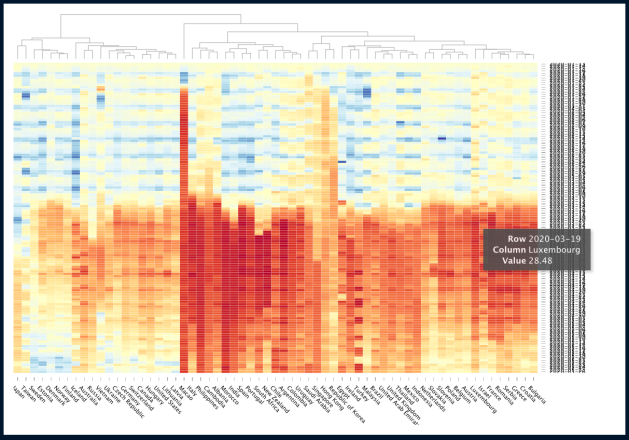
USA COVID-19 data

Here data for the USA COVID-19 infection cases and deaths from [NYT1] (see [AA6] data ingestion details):

lsCases = {1, 1, 1, 2, 3, 5, 5, 5, 5, 6, 7, 8, 11, 11, 11, 12, 12, 12,12, 12, 13, 13, 14, 15, 15, 15, 15, 25, 25, 25, 27, 30, 30, 30, 43, 45, 60, 60, 65, 70, 85, 101, 121, 157, 222, 303, 413, 530, 725,976, 1206, 1566, 2045, 2603, 3240, 4009, 5222, 6947, 9824, 13434, 17918, 23448, 30082, 37696, 46791, 59678, 73970, 88796, 103318, 119676, 139165, 160159, 184764, 212033, 241127, 262275, 288195, 314991, 341540, 370689, 398491, 423424, 445213, 467106, 490170, 512972, 539600, 566777, 590997, 613302, 637812, 660549, 685165, 714907, 747741, 777098, 800341, 820764, 844225, 868644, 895924, 927372, 953923, 977395, 998136, 1020622, 1043873, 1069587, 1095405,1118643, 1137145, 1155671, 1176913, 1196485, 1222057, 1245777, 1267911, 1285105, 1306316, 1326559, 1349019, 1373255, 1395981, 1416682, 1436260, 1455183, 1473813, 1491974, 1513223, 1536848, 1559020, 1578876, 1600414, 1620096, 1639677, 1660303, 1688335, 1709852, 1727711, 1745546, 1763803, 1784049, 1806724, 1831494, 1855870, 1874023, 1894074, 1918373, 1943743, 1970066, 2001470, 2031613, 2057493, 2088420, 2123068, 2159633, 2199841, 2244876, 2286401, 2324563, 2362875, 2411709, 2461341, 2514500, 2573030, 2622980, 2667278, 2713656, 2767129, 2825865, 2885325, 2952393, 3012349, 3069369, 3129738, 3194944, 3263077, 3338308, 3407962, 3469137, 3529938, 3588229, 3653114, 3721574, 3790356, 3862588, 3928575, 3981476, 4039440, 4101329, 4167741, 4235717, 4303663, 4359188, 4408708, 4455340, 4507370, 4560539, 4617036, 4676822, 4730639, 4777548, 4823529, 4876038, 4929115, 4981066, 5038637, 5089258, 5130147, 5166032, 5206970, 5251824, 5297150, 5344322, 5388034, 5419494, 5458726, 5497530, 5541830, 5586297, 5631403, 5674714, 5707327, 5742814, 5786178, 5817338, 5862014, 5917466, 5958619, 5988001, 6012054, 6040456, 6073671, 6110645, 6157050, 6195893, 6228601, 6264192, 6301923, 6341145, 6385411, 6432677, 6472474, 6507345, 6560827, 6597281, 6638806, 6682079, 6734971, 6776512, 6812354, 6847745, 6889421, 6930523, 6975693, 7027692, 7073962, 7107992, 7168298, 7210171, 7261433, 7315687, 7373073, 7422798, 7466501, 7513020, 7565839, 7625285, 7688761, 7757326, 7808123, 7853753, 7916879, 7976530, 8039653, 8113165, 8193658, 8270925, 8328369, 8401001, 8473618, 8555199, 8642599, 8737995, 8814233, 8892933, 8983153, 9074711, 9182627, 9301455, 9436244, 9558668, 9659817, 9784920, 9923082, 10065150, 10222441, 10405550, 10560047, 10691686, 10852769, 11011484, 11183982, 11367840, 11561152, 11727724, 11864571, 12039323, 12213742, 12397014, 12495699, 12693598, 12838076, 12972986, 13135728, 13315143, 13516558, 13728192, 13958512, 14158135, 14325555, 14519697, 14731424, 14954596, 15174109, 15447371, 15647963, 15826415, 16020169, 16218331, 16465552, 16697862, 16941306, 17132902, 17305013, 17498382, 17694678, 17918870, 18106293, 18200349, 18410644, 18559596, 18740591, 18932346, 19157710};

lsDeaths = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 6, 10, 12, 12, 15, 19, 22, 26, 31, 37, 43, 50, 59, 63, 84, 106, 137, 181, 223, 284, 335, 419, 535, 694, 880, 1181, 1444, 1598, 1955, 2490, 3117, 3904, 4601, 5864, 6408, 7376, 8850, 10159, 11415,12924, 14229, 15185, 16320, 18257, 20168, 21941, 23382, 24617, 26160, 27535, 29821, 31633, 33410, 35104, 36780, 37660, 38805, 40801, 42976, 44959, 46552, 48064, 49122, 50012, 52079, 54509, 56277, 57766, 59083, 59903, 60840, 62299, 63961, 65623, 67143, 68260, 68959, 69633, 71042, 72474, 73718, 74907, 75891, 76416, 76888, 77579, 79183, 80329, 81452, 82360, 82904, 83582, 84604, 85545, 86487, 87559, 88256, 88624, 89235, 90220, 91070, 91900, 92621, 93282, 93578, 93988, 94710, 95444, 96123, 96760, 97297, 97514, 97832, 98638, 99372, 101807, 102525, 103018, 103258, 103594,104257, 104886, 105558, 106148, 106388, 106614, 106998, 107921, 108806, 109705, 110522, 111177, 111567, 111950, 112882, 113856, 114797, 115695, 116458, 116854, 117367, 118475, 119606, 120684, 121814, 122673, 123105, 124782, 126089, 127465, 128720, 130131, 131172, 131584, 132174, 133517, 134756, 135271, 136584, 137547, 138076, 138601, 140037, 141484, 142656, 143793, 144819, 145315, 145831, 147148, 148517, 149550, 150707, 151641, 152065, 152551, 153741, 154908, 156026, 157006, 157869, 158235, 158714, 159781, 160851, 161916, 162869, 163573, 163970, 164213, 164654, 165811, 166713, 167913, 168594, 168990, 169423, 170674, 171663, 172493, 173408, 174075, 174281, 174689, 175626, 176698, 177559, 178390, 179145, 179398, 179736, 180641, 181607, 182455, 183282, 183975, 184298, 184698, 185414, 186359, 187280, 188168, 188741, 189165, 189501, 190312, 191267, 192077, 192940, 193603, 193976, 194481, 195405, 196563, 197386, 198271, 199126, 199462, 199998, 200965, 201969, 202958, 203878, 204691, 205119, 205623, 206757, 208331, 209417, 210829, 211838, 212277, 212989, 214442, 215872, 217029, 218595, 219791, 220402, 221165, 222750, 224641, 226589, 228452, 229868, 230695, 231669, 233856, 236127, 237284, 238636, 239809, 240607, 241834, 244430, 247258, 250102, 252637, 254784, 255857, 257282, 260038, 263240, 266144, 268940, 271172, 272499, 274082, 277088, 280637, 283899, 286640, 289168, 290552, 292346, 295549, 298953, 301713, 302802, 304403, 305581, 307396, 310994, 314654};

Remark: The COVID-19 data was ingested from [NYT1] on 2020-12-31,

Calibration targets

From the data we make the calibration targets association:

aTargets = <|{ISSP -> 0.2 lsCases, INSP -> 0.8 lsCases, DIP -> lsDeaths}|>;

Remark: Note that we split the infection cases into 20% severely symptomatic cases and 80% normally symptomatic cases.

Here is the corresponding plot:

ListLogPlot[aTargets, PlotTheme -> "Detailed", PlotLabel -> "Calibration targets", ImageSize -> Medium]

Here we prepare a smaller set of the targets data for the calibration experiments below:

aTargetsShort = Take[#, 170] & /@ aTargets;

Model creation

modelSEI2HR = SEI2HRModel[t, "TotalPopulationRepresentation" -> "AlgebraicEquation"];

Here are the parameters we want to experiment with (or do calibration with):

lsFocusParams = {aincp, aip, sspf[SP], \[Beta][HP], qsd, ql, qcrf, nhbcr[ISSP, INSP], nhbr[TP]};

Here we set custom rates and initial conditions:

aDefaultPars = <|     \[Beta][ISSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],      \[Beta][INSP] -> 0.5*Piecewise[{{1, t < qsd}, {qcrf, qsd <= t <= qsd + ql}}, 1],      qsd -> 60,      ql -> 8*7,      qcrf -> 0.25,      \[Beta][HP] -> 0.01,      \[Mu][ISSP] -> 0.035/aip,      \[Mu][INSP] -> 0.01/aip,      nhbr[TP] -> 3/1000,      lpcr[ISSP, INSP] -> 1,      hscr[ISSP, INSP] -> 1     |>;

Remark: Note the piecewise functions for (\beta [\text{ISSP}]) and (\beta [\text{INSP}]).

Calibration

Here is the USA population number we use for calibration:

usaPopulation = QuantityMagnitude@CountryData["UnitedStates", "Population"]  (*329064917*)

Here is we create a ECMMon object that has default parameters and initial conditions assigned above:

AbsoluteTiming[   ecmObj3 =      ECMMonUnit[]⟹      ECMMonSetSingleSiteModel[modelSEI2HR]⟹      ECMMonAssignInitialConditions[<|TP[0] -> usaPopulation, SP[0] -> usaPopulation - 1, ISSP[0] -> 1|>]⟹      ECMMonAssignRateRules[KeyDrop[aDefaultPars, {aip, aincp, qsd, ql, qcrf}]]⟹      ECMMonCalibrate[       "Target" -> KeyTake[aTargetsShort, {ISSP, DIP}],        "StockWeights" -> <|ISSP -> 0.8, DIP -> 0.2|>,        "Parameters" -> <|aip -> {10, 35}, aincp -> {2, 16}, qsd -> {60, 120}, ql -> {20, 160}, qcrf -> {0.1, 0.9}|>,        DistanceFunction -> EuclideanDistance,        Method -> {"NelderMead", "PostProcess" -> False},        MaxIterations -> 1000       ];   ]  (*{28.0993, Null}*)

Here are the found parameters:

calRes = ecmObj3⟹ECMMonTakeValue  (*{152516., {aip -> 10., aincp -> 3.67018, qsd -> 81.7067, ql -> 111.422, qcrf -> 0.312499}}*)

Using different minimization methods and distance functions

In the monad the calibration of the models is done with NMinimize. Hence, the monad function ECMMonCalibrate takes all options of NMinimize and can do calibrations with the same data and parameter search space using different global minima finding methods and distance functions.

Remark: EuclideanDistance is an obvious distance function, but use others like infinity norm and sum norm. Also, we can use a distance function that takes parts of the data. (E.g. between days 50 and 150 because the rest of the data is, say, unreliable.)

Verification of the fit

maxTime = Length[aTargets[[1]]];

ecmObj4 =     ECMMonUnit[]⟹     ECMMonSetSingleSiteModel[modelSEI2HR]⟹     ECMMonAssignInitialConditions[<|TP[0] -> usaPopulation, SP[0] -> usaPopulation - 1, ISSP[0] -> 1|>]⟹     ECMMonAssignRateRules[Join[aDefaultPars, Association[calRes[[2]]]]]⟹     ECMMonSimulate[maxTime]⟹     ECMMonPlotSolutions[___ ~~ "Population" ~~ ___, maxTime, ImageSize -> Large, LogPlot -> False];

aSol4 = ecmObj4⟹ECMMonGetSolutionValues[Keys[aTargets], maxTime]⟹ECMMonTakeValue;

Map[ListLogPlot[{aSol4[#], aTargets[#]}, PlotLabel -> #, PlotRange -> All, ImageSize -> Medium, PlotLegends -> {"Calibrated model", "Target"}] &, Keys[aTargets]]

Conclusions from the calibration results

We see the that with the calibration found parameter values the model can fit the data for the first 200 days, after that it overestimates the evolution of the infected and deceased popupulations.

We can conjecture that:

The model is too simple, hence inadequate
That more complicated quarantine policy functions have to be used
That the calibration process got stuck in some local minima

Future plans

In this section we outline some of the directions in which the presented work on ECMMon can be extended.

More unit tests and random unit tests

We consider the preparation and systematic utilization of unit tests to be a very important component of any software development. Unit tests are especially important when complicated software package like ECMMon are developed.

For the presented software monad (and its separately developed, underlying packages) have implemented a few collections of tests, see [AAp10, AAp11].

We plan to extend and add more complicated unit tests that test for both quantitative and qualitative behavior. Here are some examples for such tests:

Stock-vs-stock orbits produced by simulations of certain epidemic models
Expected theoretical relationships between populations (or other stocks) for certain initial conditions and rates
Wave-like propagation of the proportions of the infected populations in multi-site models over artificial countries and traveling patterns
Finding of correct parameter values with model calibration over different data (both artificial and real life)
Expected number of equations for different model set-ups
Expected (relative) speed of simulations with respect to model sizes

Further for the monad ECMMon we plant to develop random pipeline unit tests as the ones in [AAp12] for the classification monad ClCon, [AA11].

Full correspondence between the Mathematica and R implementations

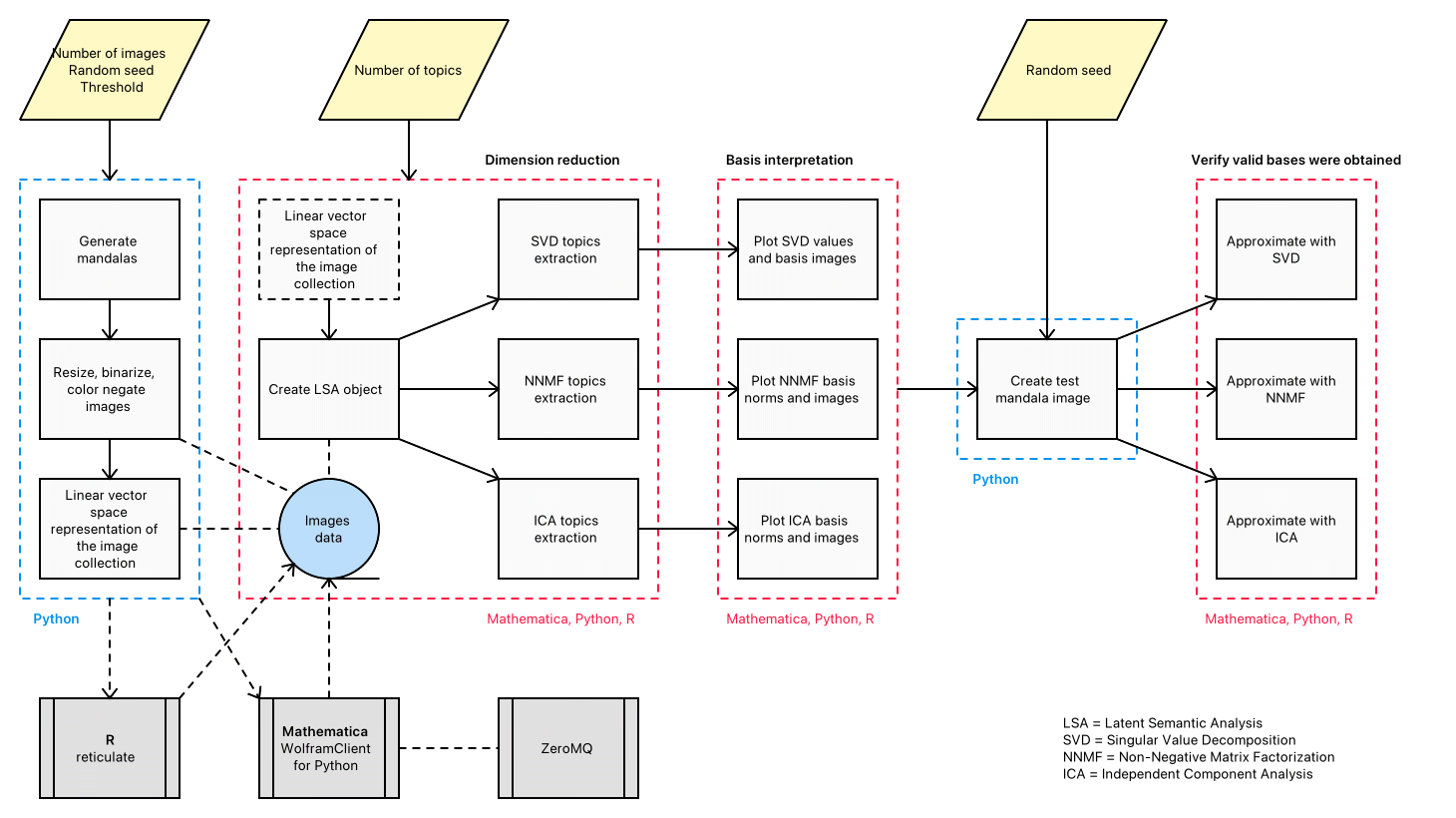
The ingredients of the software monad ECMMon and ECMMon itself were designed and implemented in Mathematica first. The corresponding design and implementation was done in R, [AAr2]. To distinguish the two implementations we call the R one ECMMon-R and Mathematica (Wolfram Language) one ECMMon-WL.

At this point the calibration is not implemented in ECMMon-R, but we plan to do that soon.

Using ECMMon-R (and the RStudio’s Shiny ecosystem) allows for highly shareable interactive interfaces to be programed. Here is an example: https://antononcube.shinyapps.io/SEI2HR-flexdashboard/ .

(With Mathematica similar interactive interfaces are presented in [AA7, AA8].)

Model transfer between Mathematica and R

We are very interested in transferring epidemiological models from Mathematica to R (or Python, or Julia.)

This can be done in two principle ways: (i) using Mathematica expressions parsers, or (ii) using matrix representations. We plan to investigate the usage of both approaches.

Conversational agent

Consider the making of a conversational agent for epidemiology modeling workflows building. Initial design and implementation is given in [AA13, AA14].

Consider the following epidemiology modeling workflow specification:

lsCommands = "create with SEI2HR;assign 100000 to total population;set infected normally symptomatic population to be 0;set infected severely symptomatic population to be 1;assign 0.56 to contact rate of infected normally symptomatic population;assign 0.58 to contact rate of infected severely symptomatic population;assign 0.1 to contact rate of the hospitalized population;simulate for 240 days;plot populations results;calibrate for target DIPt -> tsDeaths, over parameters contactRateISSP in from 0.1 to 0.7;echo pipeline value";

Here is the ECMMon code generated using the workflow specification:

ToEpidemiologyModelingWorkflowCode[lsCommands, "Execute" -> False, "StringResult" -> True]  (*"ECMMonUnit[SEI2HRModel[t]] ⟹ECMMonAssignInitialConditions[<|TP[0] -> 100000|>] ⟹ECMMonAssignInitialConditions[<|INSP[0] -> 0|>] ⟹ECMMonAssignInitialConditions[<|ISSP[0] -> 1|>] ⟹ECMMonAssignRateRules[<|\\[Beta][INSP] -> 0.56|>] ⟹ECMMonAssignRateRules[<|\\[Beta][ISSP] -> 0.58|>] ⟹ECMMonAssignRateRules[<|\\[Beta][HP] -> 0.1|>] ⟹ECMMonSimulate[\"MaxTime\" -> 240] ⟹ECMMonPlotSolutions[ \"Stocks\" -> __ ~~ \"Population\"] ⟹ECMMonCalibrate[ \"Target\" -> <|DIP -> tsDeaths|>, \"Parameters\" -> <|\\[Beta][ISSP] -> {0.1, 0.7}|> ] ⟹ECMMonEchoValue[]"*)

Here is the execution of the code above:

Block[{tsDeaths = Take[lsDeaths, 150]}, ToEpidemiologyModelingWorkflowCode[lsCommands]];

Different target languages

Using the natural commands workflow specification we can generate code to other languages, like, Python or R:

ToEpidemiologyModelingWorkflowCode[lsCommands, "Target" -> "Python"]  (*"obj = ECMMonUnit( model = SEI2HRModel())obj = ECMMonAssignInitialConditions( ecmObj = obj, initConds = [TPt = 100000])obj = ECMMonAssignInitialConditions( ecmObj = obj, initConds = [INSPt = 0])obj = ECMMonAssignInitialConditions( ecmObj = obj, initConds = [ISSPt = 1])obj = ECMMonAssignRateValues( ecmObj = obj, rateValues = [contactRateINSP = 0.56])obj = ECMMonAssignRateValues( ecmObj = obj, rateValues = [contactRateISSP = 0.58])obj = ECMMonAssignRateValues( ecmObj = obj, rateValues = [contactRateHP = 0.1])obj = ECMMonSimulate( ecmObj = obj, maxTime = 240)obj = ECMMonPlotSolutions( ecmObj = obj, stocksSpec = \".*Population\")obj = ECMMonCalibrate( ecmObj = obj,  target = [DIPt = tsDeaths], parameters = [contactRateISSP = [0.1, 0.7]] )"*)

References

Articles

[Wk1] Wikipedia entry, Monad.

[Wk2] Wikipedia entry, “Compartmental models in epidemiology”.

[Wk3] Wikipedia entry, “Coronavirus disease 2019”.

[BC1] Lucia Breierova, Mark Choudhari, An Introduction to Sensitivity Analysis, (1996), Massachusetts Institute of Technology.

[JS1] John D.Sterman, Business Dynamics: Systems Thinking and Modeling for a Complex World. (2000), New York: McGraw.

[HH1] Herbert W. Hethcote (2000). “The Mathematics of Infectious Diseases”. SIAM Review. 42 (4): 599–653. Bibcode:2000SIAMR..42..599H. doi:10.1137/s0036144500371907.

[AA1] Anton Antonov, ”Monad code generation and extension”, (2017), MathematicaForPrediction at GitHub/antononcube.

[AA2] Anton Antonov, “Coronavirus propagation modeling considerations”, (2020), SystemModeling at GitHub/antononcube.

[AA3] Anton Antonov, “Basic experiments workflow for simple epidemiological models”, (2020), SystemModeling at GitHub/antononcube.

[AA4] Anton Antonov, “Scaling of Epidemiology Models with Multi-site Compartments”, (2020), SystemModeling at GitHub/antononcube.

[AA5] Anton Antonov, “WirVsVirus hackathon multi-site SEI2R over a hexagonal grid graph”, (2020), SystemModeling at GitHub/antononcube.

[AA6] Anton Antonov, “NY Times COVID-19 data visualization”, (2020), SystemModeling at GitHub/antononcube.

[AA7] Anton Antonov, “SEI2HR model with quarantine scenarios”, (2020), SystemModeling at GitHub/antononcube.

[AA8] Anton Antonov, “SEI2HR-Econ model with quarantine and supplies scenarios”, (2020), SystemModeling at GitHub/antononcube.

[AA9] Anton Antonov, Modelers questionnaire, (2020), SystemModeling at GitHub/antononcube.

[AA10] Anton Antonov, Calibrators questionnaire, (2020), SystemModeling at GitHub/antononcube.

[AA11] Anton Antonov, A monad for classification workflows, (2018), MathematicaForPrediction at WordPress.

Repositories, packages

[WRI1] Wolfram Research, Inc., “Epidemic Data for Novel Coronavirus COVID-19”, WolframCloud.

[WRI2] Wolfram Research Inc., USA county records, (2020), System Modeling at GitHub.

[NYT1] The New York Times, Coronavirus (Covid-19) Data in the United States, (2020), GitHub.

[AAr1] Anton Antonov, Coronavirus propagation dynamics project, (2020), SystemModeling at GitHub/antononcube.

[AAr2] Anton Antonov, Epidemiology Compartmental Modeling Monad R package, (2020), ECMMon-R at GitHu/antononcube.

[AAp1] Anton Antonov, State monad code generator Mathematica package, (2017), MathematicaForPrediction at GitHub/antononcube.

[AAp2] Anton Antonov, Monadic tracing Mathematica package, (2017), MathematicaForPrediction at GitHub/antononcube.

[AAp3] Anton Antonov, Epidemiology models Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp4] Anton Antonov, Epidemiology models modifications Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp5] Anton Antonov, Epidemiology modeling visualization functions Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp6] Anton Antonov, System dynamics interactive interfaces functions Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp7] Anton Antonov, Multi-site model simulation Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp8] Anton Antonov, Monadic Epidemiology Compartmental Modeling Mathematica package, (2020), SystemModeling at GitHub/antononcube.

[AAp9] Anton Antonov, Hextile bins Mathematica package, (2020), MathematicaForPrediction at GitHub/antononcube.

[AAp10] Anton Antonov, Monadic Epidemiology Compartmental Modeling Mathematica unit tests, (2020), SystemModeling at GitHub/antononcube.

[AAp11] Anton Antonov, Epidemiology Models NDSolve Mathematica unit tests, (2020), SystemModeling at GitHub/antononcube.

[AAp12] Anton Antonov, Monadic contextual classification random pipelines Mathematica unit tests, (2018), MathematicaForPrediction at GitHub/antononcube.

[AAp13] Anton Antonov, Epidemiology Modeling Workflows Raku package, (2020), Raku-DSL-English-EpidemiologyModelingWorkflows at GitHu/antononcube.

[AAp14] Anton Antonov, External Parsers Hookup Mathematica package, (2019), ConversationalAgents at GitHub.

Investigating COVID-19 with R: data analysis and simulations

Posted on May 29, 2020 by Anton Antonov Antonov

Methodological presentation
R-Ladies Miami Meetup, May 28th 2020

The extended abstract of the presentation was loosely followed. Here is the presentation mind-map:

(Note that mind-map’s PDF has hyperlinks. Also, see the folder Presentation-aids. )

The organizers and I did a poll for what people want to hear. After discussing the results of the 15 votes from that poll we decided the presentation to be a methodological one instead of a know-how one.

Approximately 30% of the presentation was based on the R-project “COVID-19-modeling-in-R”, [AA1].

Approximately 30% of the presentation was based on an R-programmed software monad for epidemiology compartmental models, ECMMon-R, [AAr2].

For the rest were used frameworks, simulations, and graphics made with Mathematica, [AAr1].

The presentation was given online (because of COVID-19) using Zoom. 90 people registered. Nearly 40 showed up (and maybe 20 stayed throughout.)

Here is a link to the video recording.

Screenshots

Here are screenshots of statistics used in the introduction:

References

Coronavirus

[Wk1] Wikipedia entry, Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2).

[Wk2] Wikipedia entry, Coronavirus disease 2019.

Modeling

[Wk3] Wikipedia entry, Compartmental models in epidemiology.

[Wk4] Wikipedia entry, System dynamics.

R code/software

[KS1] Karline Soetaert, Thomas Petzoldt, R. Woodrow Setzer, “deSolve: Solvers for Initial Value Problems of Differential Equations (‘ODE’, ‘DAE’, ‘DDE’)”, CRAN.

[AA1] Anton Antonov, “COVID-19-modeling-in-R”, 2020, SystemModeling at GitHub.

[AAr1] Anton Antonov, Coronavirus-propagation-dynamics, 2020, SystemModeling at GitHub.

[AAr2] Anton Antonov, Epidemiology Compartmental Modeling Monad in R, 2020, ECMMon-R at GitHub.

Coronavirus propagation modeling, useR! Boston April 2020

Posted on April 15, 2020 by Anton Antonov Antonov

Tutorial presentation

The extended abstract of the presentation was loosely followed. Here is the (main) presentation mind-map:

(Note that mind-map’s PDF has hyperlinks. Also, see the folder Presentation-aids. )

Approximately 70% of the presentation was based on an R-programmed software monad for epidemiology compartmental models, ECMMon-R, [AAr2]. For the rest were used frameworks, simulations, and graphics made with Mathematica, [AAr1], and Wolfram System Modeler .

The presentation was given online (because of COVID-19) using Zoom. 190 people registered. Nearly 70 showed up (and maybe 60 stayed throughout.)

Here is a link to the video recording.

A similar presentation was given two weeks prior for OMLDS.

References

Coronavirus

[Wk1] Wikipedia entry, Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2).

[Wk2] Wikipedia entry, Coronavirus disease 2019.

Modeling

[Wk3] Wikipedia entry, Compartmental models in epidemiology.

[Wk4] Wikipedia entry, System dynamics.

[JD1] Jim Duggan, System Dynamics Modeling with R, 2016, Springer.

R code/software

[KS1] Karline Soetaert, Thomas Petzoldt, R. Woodrow Setzer, “deSolve: Solvers for Initial Value Problems of Differential Equations (‘ODE’, ‘DAE’, ‘DDE’)”, CRAN.

[JD2] Jim Duggan, “SDMR”, 2016, GitHub.
(Resources for text book “System Dynamics Modeling with R”.)

[AA1] Anton Antonov, “COVID-19-modeling-in-R”, 2020, SystemModeling at GitHub.

[AAr1] Anton Antonov, Coronavirus-propagation-dynamics, 2020, SystemModeling at GitHub.

[AAr2] Anton Antonov, Epidemiology Compartmental Modeling Monad in R, 2020, ECMMon-R at GitHub.

WirVsVirus 2020 hackathon participation

Posted on March 24, 2020 by Anton Antonov Antonov

Introduction

Last weekend – 2020-03-20 ÷ 2020-03-22 – I participated in the (Germany-centric) hackathon WirVsVirus. (I friend of mine who lives in Germany asked me to team up and sign up.)

Our idea proposal was accepted, listed in the dedicated overview table (see item 806). The title of our hackathon project is:

“Geo-spatial-temporal Economic Model for COVID-19 Propagation and Management in Germany”

Nearly a dozen of people enlisted to help. (We communicated through Slack.)

WebImage["https://devpost.com/software/geo-raumlich-zeitliches-\
wirtschaftsmodell-fur-covid-19"]

Multiple people helped with the discussion of ideas, directions where to find data, with actual data gathering, and related documented analysis. Of course, just discussing the proposed solutions was already a great help!

What was accomplished

Work plans

The following mind-map reflects pretty well what was planned and done:

There is also a related org-mode file with the work plan.

Data

I obtained Germany city data with Mathematica’s build-in functions and used it to heuristically derive a traveling patterns graph, [AA1].

Here is the data:

dsCityRecords = 
  ResourceFunction["ImportCSVToDataset"][
   "https://raw.githubusercontent.com/antononcube/SystemModeling/\
master/Data/dfGermanyCityRecords.csv"];
Dimensions[dsCityRecords]

(*{12538, 6}*)

Here is Geo-histogram of that data:

aCoordsToPopulations = 
  AssociationThread[
   Values /@ Normal[dsCityRecords[All, {"Lat", "Lon"}]], 
   Normal[dsCityRecords[All, "Population"]]];
grHist = GeoHistogram[aCoordsToPopulations, cellRadius, 
   ColorFunction -> (Opacity[#, Blue] &), PlotLegends -> Automatic];
If[TrueQ[renderGraphPlotsQ], grHist]

We considered a fair amount of other data. But because of the time limitations of the hackathon we had to use only the one above.

Single-site models

During the development phase I used the model SEI2R, but since we wanted to have a “geo-spatial-temporal epidemiological economics model” I productized the implementation of SEI2HR-Econ, [AAp1].

Here are the stocks, rates, and equations of SEI2HR-Econ:

Magnify[ModelGridTableForm[SEI2HREconModel[t]], 0.85]

Multi-site SEI2R (SEI2HR-Econ) over a hexagonal grid graph

I managed to follow through with a large part of the work plan for the hackathon and make multi-site scaled model that “follows the money”, [AA1]. Here is a diagram that shows the travelling patterns graph and solutions at one of the nodes:

Here is (a snapshot of) an interactive interface for studying and investigating the solution results:

For more details see the notebook [AA1]. Different parameters can be set in the “Parameters” section. Especially of interest are the quarantine related parameters: start, duration, effect on contact rates and traffic patterns.

I also put in that notebook code for exporting simulations results and programmed visualization routines in R, [AA2]. (In order other members of team to be able to explore the results.)

References

[DP1] 47_wirtschaftliche Auswirkung_Geo-spatial-temp-econ-modell, DevPost.

[WRI1] Wolfram Research, Inc., Germany city data records, (2020), SystemModeling at GitHub.

[AA1] Anton Antonov, “WirVsVirus hackathon multi-site SEI2R over a hexagonal grid graph”, (2020), SystemModeling at GitHub.

[AA2] Anton Antonov, “WirVsVirus-Hackathon in R”, (2020), SystemModeling at GitHub.

[AAp1] Anton Antonov, “Epidemiology models Mathematica package”, (2020), SystemsModeling at GitHub.

Mathematica-vs-R: Deep learning examples

Posted on June 15, 2018 by Anton Antonov Antonov

Introduction

This MathematicaVsR at GitHub project is for the comparison of the Deep Learning functionalities in R/RStudio and Mathematica/Wolfram Language (WL).

The project is aimed to mirror and aid the talk "Deep Learning series (session 2)" of the meetup Orlando Machine Learning and Data Science.

The focus of the talk is R and Keras, so the project structure is strongly influenced by the content of the book Deep learning with R, [1], and the corresponding Rmd notebooks, [2].

Some of Mathematica’s notebooks repeat the material in [2]. Some are original versions.

WL’s Neural Nets framework and abilities are fairly well described in the reference page "Neural Networks in the Wolfram Language overview", [4], and the webinar talks [5].

The corresponding documentation pages [3] (R) and [6] (WL) can be used for a very fruitful comparison of features and abilities.

Remark: With "deep learning with R" here we mean "Keras with R".

Remark: An alternative to R/Keras and Mathematica/MXNet is the library H2O (that has interfaces to Java, Python, R, Scala.) See project’s directory R.H2O for examples.

The presentation

Mind map for the presentation. (Has life hyperlinks.)
Presentation slideshow: html, Rpres.
"Neural network layers primer" slideshow.
The slideshow is part of Sebastian Bodenstein’s presentation at Wolfram U.
(It was separated/extracted for clarity and convenience during the meetup presentation.)
Recording of the presentation at YouTube:
ORLMLDS Deep learning series (2): "Using Keras with R (… and MXNet with WL)".
The info-chart "Classification of handwritten digits by matrix factorization" (used in the presentation.)

The big picture

Deep learning can be used for both supervised and unsupervised learning. In this project we concentrate on supervised learning.

The following diagram outlines the general, simple classification workflow we have in mind.

Here is a corresponding classification monadic pipeline in Mathematica:

monadic_pipeline

Code samples

R-Keras uses monadic pipelines through the library magrittr. For example:

model <- keras_model_sequential() 
model %>% 
  layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>% 
  layer_dropout(rate = 0.4) %>% 
  layer_dense(units = 128, activation = 'relu') %>%
  layer_dropout(rate = 0.3) %>%
  layer_dense(units = 10, activation = 'softmax')

The corresponding Mathematica command is:

model =
 NetChain[{
   LinearLayer[256, "Input" -> 784],
   ElementwiseLayer[Ramp],            
   DropoutLayer[0.4],
   LinearLayer[128],
   ElementwiseLayer[Ramp],            
   DropoutLayer[0.3],
   LinearLayer[10]
 }]

Comparison

Installation

Mathematica
The neural networks framework comes with Mathematica. (No additional installation required.)
R
Pretty straightforward using the directions in [3]. (A short list.)
Some additional Python installation is required.

Simple neural network classifier over MNIST data

Mathematica: Simple-neural-network-classifier-over-MNIST-data.pdf
R-Keras: Keras-with-R-talk-introduction.nb.html, Keras-with-R-talk-introduction.Rmd.

Vector classification

TBD…

Categorical classification

TBD…

Regression

Mathematica: Predicting-house-prices-a-regression-example.pdf.
R-Keras: 3.6-predicting-house-prices.nb.html, 3.6-predicting-house-prices.Rmd.
(Those are links to notebooks in [2].)

Encoders and decoders

The Mathematica encoders (for neural networks and generally for machine learning tasks) are very well designed and with a very advanced development.

The encoders in R-Keras are fairly useful but not was advanced as those in Mathematica.

[TBD: Encoder correspondence…]

Dealing with over-fitting

Mathematica: Training-Neural-Networks-with-Regularization.pdf.
R-Keras: Training-Neural-Networks-with-Regularization.nb.html, Training-Neural-Networks-with-Regularization.Rmd.

Repositories of pre-trained models

Mathematica: Wolfram Research repository of neural networks; can import externally trained networks in MXNet format.
R-Keras: has commands loading for pre-trained models, [3].

Documentation

Mathematica: "Neural Networks guide".
R-Keras: "Keras reference", cheatsheet.

References

[1] F. Chollet, J. J. Allaire, Deep learning with R, (2018).

[2] J. J. Allaire, Deep Learing with R notebooks, (2018), GitHub.

[3] RStudio, Keras reference.

[4] Wolfram Research, "Neural Networks in the Wolfram Language overview".

[5] Wolfram Research, "Machine Learning Webinar Series".

[6] Wolfram Research, "Neural Networks guide".

Progressive Machine Learning Examples

Posted on April 13, 2018 by Anton Antonov Antonov

Introduction

In this MathematicaVsR at GitHub project we show how to do Progressive machine learning using two types of classifiers based on:

Tries with Frequencies, [AAp2, AAp3, AA1],
Sparse Matrix Recommender framework [AAp4, AA2].

Progressive learning is a type of Online machine learning. For more details see [Wk1]. The Progressive learning problem is defined as follows.

Problem definition:

Assume that the data is sequentially available.
- Meaning, at a given time only part of the data is available, and after a certain time interval new data can be obtained.
- In view of classification, it is assumed that at a given time not all class labels are presented in the data already obtained.
- Let us call this a data stream.
Make a machine learning algorithm that updates its model continuously or sequentially in time over a given data stream.
- Let us call such an algorithm a Progressive Learning Algorithm (PLA).

In comparison, the typical (classical) machine learning algorithms assume that representative training data is available and after training that data is no longer needed to make predictions. Progressive machine learning has more general assumptions about the data and its problem formulation is closer to how humans learn to classify objects.

Below we are shown the applications of two types of classifiers as PLA’s. One is based on Tries with Frequencies (TF), [AAp2, AAp3, AA1], the other on an Item-item Recommender (IIR) framework [AAp4, AA2].

Remark: Note that both TF and IIR come from tackling Unsupervised machine learning tasks, but here they are applied in the context of Supervised machine learning.

General workflow

The Mathematica and R notebooks follow the steps in the following flow chart.

For detailed explanations see any of the notebooks.

Project organization

Mathematica files

R files

Example runs

(For details see Progressive-machine-learning-examples.md.)

Using Tries with Frequencies

Here is an example run with Tries with Frequencies, [AAp2, AA1]:

Here are the obtained ROC curves:

We can see that with the Progressive learning process does improve its success rates in time.

Using an Item-item recommender system

Here is an example run with an Item-item recommender system, [AAp4, AA2]:

Here are the obtained ROC curves:

References

Packages

[AAp1] Anton Antonov, Obtain and transform Mathematica machine learning data-sets, GetMachineLearningDataset.m, (2018), MathematicaVsR at GitHub.

[AAp2] Anton Antonov, Java tries with frequencies Mathematica package, JavaTriesWithFrequencies.m, (2017), MathematicaForPrediction at GitHub.

[AAp3] Anton Antonov, Tries with frequencies R package, TriesWithFrequencies.R, (2014), MathematicaForPrediction at GitHub.

[AAp4] Anton Antonov, Sparse matrix recommender framework in Mathematica, SparseMatrixRecommenderFramework.m, (2014), MathematicaForPrediction at GitHub.

Articles

[Wk1] Wikipedia entry, Online machine learning.

[AA1] Anton Antonov, "Tries with frequencies in Java", (2017), MathematicaForPrediction at WordPress.

[AA2] Anton Antonov, "A Fast and Agile Item-Item Recommender: Design and Implementation", (2011), Wolfram Technology Conference 2011.

Monad code generation and extension

Posted on June 23, 2017 by Anton Antonov Antonov

… in Mathematica / Wolfram Language

Anton Antonov

MathematicaForPrediction at GitHub

MathematicaVsR at GitHub

June 2017

Introduction

This document aims to introduce monadic programming in Mathematica / Wolfram Language (WL) in a concise and code-direct manner. The core of the monad codes discussed is simple, derived from the fundamental principles of Mathematica / WL.

The usefulness of the monadic programming approach manifests in multiple ways. Here are a few we are interested in:

easy to construct, read, and modify sequences of commands (pipelines),
easy to program polymorphic behaviour,
easy to program context utilization.

Speaking informally,

Monad programming provides an interface that allows interactive, dynamic creation and change of sequentially structured computations with polymorphic and context-aware behavior.

The theoretical background provided in this document is given in the Wikipedia article on Monadic programming, [Wk1], and the article “The essence of functional programming” by Philip Wadler, [H3]. The code in this document is based on the primary monad definition given in [Wk1,H3]. (Based on the “Kleisli triple” and used in Haskell.)

The general monad structure can be seen as:

a software design pattern;
a fundamental programming construct (similar to class in object-oriented programming);
an interface for software types to have implementations of.

In this document we treat the monad structure as a design pattern, [Wk3]. (After reading [H3] point 2 becomes more obvious. A similar in spirit, minimalistic approach to Object-oriented Design Patterns is given in [AA1].)

We do not deal with types for monads explicitly, we generate code for monads instead. One reason for this is the “monad design pattern” perspective; another one is that in Mathematica / WL the notion of algebraic data type is not needed — pattern matching comes from the core “book of replacement rules” principle.

The rest of the document is organized as follows.

1. Fundamental sections The section “What is a monad?” gives the necessary definitions. The section “The basic Maybe monad” shows how to program a monad from scratch in Mathematica / WL. The section “Extensions with polymorphic behavior” shows how extensions of the basic monad functions can be made. (These three sections form a complete read on monadic programming, the rest of the document can be skipped.)

2. Monadic programming in practice The section “Monad code generation” describes packages for generating monad code. The section “Flow control in monads” describes additional, control flow functionalities. The section “General work-flow of monad code generation utilization” gives a general perspective on the use of monad code generation. The section “Software design with monadic programming” discusses (small scale) software design with monadic programming.

3. Case study sections The case study sections “Contextual monad classification” and “Tracing monad pipelines” hopefully have interesting and engaging examples of monad code generation, extension, and utilization.

What is a monad?

The monad definition

In this document a monad is any set of a symbol m and two operators unit and bind that adhere to the monad laws. (See the next sub-section.) The definition is taken from [Wk1] and [H3] and phrased in Mathematica / WL terms in this section. In order to be brief, we deliberately do not consider the equivalent monad definition based on unit, join, and map (also given in [H3].)

Here are operators for a monad associated with a certain symbol M:

monad unit function (“return” in Haskell notation) is Unit[x_] := M[x];
monad bind function (“>>=” in Haskell notation) is a rule like Bind[M[x_], f_] := f[x] with MatchQ[f[x],M[_]] giving True.

Note that:

the function Bind unwraps the content of M[_] and gives it to the function f;
the functions f_i are responsible to return results wrapped with the monad symbol M.

Here is an illustration formula showing a monad pipeline:

Monad-formula-generic

From the definition and formula it should be clear that if for the result of Bind[_M,f[x]] the test MatchQ[f[x],_M] is True then the result is ready to be fed to the next binding operation in monad’s pipeline. Also, it is clear that it is easy to program the pipeline functionality with Fold:

Fold[Bind, M[x], {f1, f2, f3}]

(* Bind[Bind[Bind[M[x], f1], f2], f3] *)

The monad laws

The monad laws definitions are taken from [H1] and [H3].In the monad laws given below the symbol “⟹” is for monad’s binding operation and ↦ is for a function in anonymous form.

Here is a table with the laws:

Remark: The monad laws are satisfied for every symbol in Mathematica / WL with List being the unit operation and Apply being the binding operation.

Expected monadic programming features

Looking at formula (1) — and having certain programming experiences — we can expect the following features when using monadic programming.

Computations that can be expressed with monad pipelines are easy to construct and read.
By programming the binding function we can tuck-in a variety of monad behaviours — this is the so called “programmable semicolon” feature of monads.
Monad pipelines can be constructed with Fold, but with suitable definitions of infix operators like DoubleLongRightArrow (⟹) we can produce code that resembles the pipeline in formula (1).
A monad pipeline can have polymorphic behaviour by overloading the signatures of f_i (and if we have to, Bind.)

These points are clarified below. For more complete discussions see [Wk1] or [H3].

The basic Maybe monad

It is fairly easy to program the basic monad Maybe discussed in [Wk1].

The goal of the Maybe monad is to provide easy exception handling in a sequence of chained computational steps. If one of the computation steps fails then the whole pipeline returns a designated failure symbol, say None otherwise the result after the last step is wrapped in another designated symbol, say Maybe.

Here is the special version of the generic pipeline formula (1) for the Maybe monad:

“Monad-formula-maybe”

Here is the minimal code to get a functional Maybe monad (for a more detailed exposition of code and explanations see [AA7]):

MaybeUnitQ[x_] := MatchQ[x, None] || MatchQ[x, Maybe[___]];

MaybeUnit[None] := None;
MaybeUnit[x_] := Maybe[x];

MaybeBind[None, f_] := None;
MaybeBind[Maybe[x_], f_] := 
  Block[{res = f[x]}, If[FreeQ[res, None], res, None]];

MaybeEcho[x_] := Maybe@Echo[x];
MaybeEchoFunction[f___][x_] := Maybe@EchoFunction[f][x];

MaybeOption[f_][xs_] := 
  Block[{res = f[xs]}, If[FreeQ[res, None], res, Maybe@xs]];

In order to make the pipeline form of the code we write let us give definitions to a suitable infix operator (like “⟹”) to use MaybeBind:

DoubleLongRightArrow[x_?MaybeUnitQ, f_] := MaybeBind[x, f];
DoubleLongRightArrow[x_, y_, z__] := 
  DoubleLongRightArrow[DoubleLongRightArrow[x, y], z];

Here is an example of a Maybe monad pipeline using the definitions so far:

data = {0.61, 0.48, 0.92, 0.90, 0.32, 0.11};

MaybeUnit[data]⟹(* lift data into the monad *)
 (Maybe@ Join[#, RandomInteger[8, 3]] &)⟹(* add more values *)
 MaybeEcho⟹(* display current value *)
 (Maybe @ Map[If[# < 0.4, None, #] &, #] &)(* map values that are too small to None *)

(* {0.61,0.48,0.92,0.9,0.32,0.11,4,4,0}
 None *)

The result is None because:

the data has a number that is too small, and
the definition of MaybeBind stops the pipeline aggressively using a FreeQ[_,None] test.

Monad laws verification

Let us convince ourselves that the current definition of MaybeBind gives a monad.

The verification is straightforward to program and shows that the implemented Maybe monad adheres to the monad laws.

“Monad-laws-table-Maybe”

Extensions with polymorphic behavior

We can see from formulas (1) and (2) that the monad codes can be easily extended through overloading the pipeline functions.

For example the extension of the Maybe monad to handle of Dataset objects is fairly easy and straightforward.

Here is the formula of the Maybe monad pipeline extended with Dataset objects:

Here is an example of a polymorphic function definition for the Maybe monad:

MaybeFilter[filterFunc_][xs_] := Maybe@Select[xs, filterFunc[#] &];

MaybeFilter[critFunc_][xs_Dataset] := Maybe@xs[Select[critFunc]];

See [AA7] for more detailed examples of polymorphism in monadic programming with Mathematica / WL.

A complete discussion can be found in [H3]. (The main message of [H3] is the poly-functional and polymorphic properties of monad implementations.)

Polymorphic monads in R’s dplyr

The R package dplyr, [R1], has implementations centered around monadic polymorphic behavior. The command pipelines based on dplyrcan work on R data frames, SQL tables, and Spark data frames without changes.

Here is a diagram of a typical work-flow with dplyr:

The diagram shows how a pipeline made with dplyr can be re-run (or reused) for data stored in different data structures.

Monad code generation

We can see monad code definitions like the ones for Maybe as some sort of initial templates for monads that can be extended in specific ways depending on their applications. Mathematica / WL can easily provide code generation for such templates; (see [WL1]). As it was mentioned in the introduction, we do not deal with types for monads explicitly, we generate code for monads instead.

In this section are given examples with packages that generate monad codes. The case study sections have examples of packages that utilize generated monad codes.

Maybe monads code generation

The package [AA2] provides a Maybe code generator that takes as an argument a prefix for the generated functions. (Monad code generation is discussed further in the section “General work-flow of monad code generation utilization”.)

Here is an example:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MaybeMonadCodeGenerator.m"]

GenerateMaybeMonadCode["AnotherMaybe"]

data = {0.61, 0.48, 0.92, 0.90, 0.32, 0.11};

AnotherMaybeUnit[data]⟹(* lift data into the monad *)
 (AnotherMaybe@Join[#, RandomInteger[8, 3]] &)⟹(* add more values *)
 AnotherMaybeEcho⟹(* display current value *)
 (AnotherMaybe @ Map[If[# < 0.4, None, #] &, #] &)(* map values that are too small to None *)

(* {0.61,0.48,0.92,0.9,0.32,0.11,8,7,6}
   AnotherMaybeBind: Failure when applying: Function[AnotherMaybe[Map[Function[If[Less[Slot[1], 0.4], None, Slot[1]]], Slot[1]]]]
   None *)

We see that we get the same result as above (None) and a message prompting failure.

State monads code generation

The State monad is also basic and its programming in Mathematica / WL is not that difficult. (See [AA3].)

Here is the special version of the generic pipeline formula (1) for the State monad:

“Monad-formula-State”

Note that since the State monad pipeline caries both a value and a state, it is a good idea to have functions that manipulate them separately. For example, we can have functions for context modification and context retrieval. (These are done in [AA3].)

This loads the package [AA3]:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/StateMonadCodeGenerator.m"]

This generates the State monad for the prefix “StMon”:

GenerateStateMonadCode["StMon"]

The following StMon pipeline code starts with a random matrix and then replaces numbers in the current pipeline value according to a threshold parameter kept in the context. Several times are invoked functions for context deposit and retrieval.

SeedRandom[34]
StMonUnit[RandomReal[{0, 1}, {3, 2}], <|"mark" -> "TooSmall", "threshold" -> 0.5|>]⟹
  StMonEchoValue⟹
  StMonEchoContext⟹
  StMonAddToContext["data"]⟹
  StMonEchoContext⟹
  (StMon[#1 /. (x_ /; x < #2["threshold"] :> #2["mark"]), #2] &)⟹
  StMonEchoValue⟹
  StMonRetrieveFromContext["data"]⟹
  StMonEchoValue⟹
  StMonRetrieveFromContext["mark"]⟹
  StMonEchoValue;

(* value: {{0.789884,0.831468},{0.421298,0.50537},{0.0375957,0.289442}}
   context: <|mark->TooSmall,threshold->0.5|>
   context: <|mark->TooSmall,threshold->0.5,data->{{0.789884,0.831468},{0.421298,0.50537},{0.0375957,0.289442}}|>
   value: {{0.789884,0.831468},{TooSmall,0.50537},{TooSmall,TooSmall}}
   value: {{0.789884,0.831468},{0.421298,0.50537},{0.0375957,0.289442}}
   value: TooSmall *)

Flow control in monads

We can implement dedicated functions for governing the pipeline flow in a monad.

Let us look at a breakdown of these kind of functions using the State monad StMon generated above.

Optional acceptance of a function result

A basic and simple pipeline control function is for optional acceptance of result — if failure is obtained applying f then we ignore its result (and keep the current pipeline value.)

Here is an example with StMonOption :

SeedRandom[34]
StMonUnit[RandomReal[{0, 1}, 5]]⟹
 StMonEchoValue⟹
 StMonOption[If[# < 0.3, None] & /@ # &]⟹
 StMonEchoValue

(* value: {0.789884,0.831468,0.421298,0.50537,0.0375957}
   value: {0.789884,0.831468,0.421298,0.50537,0.0375957}
   StMon[{0.789884, 0.831468, 0.421298, 0.50537, 0.0375957}, <||>] *)

Without StMonOption we get failure:

SeedRandom[34]
StMonUnit[RandomReal[{0, 1}, 5]]⟹
 StMonEchoValue⟹
 (If[# < 0.3, None] & /@ # &)⟹
 StMonEchoValue

(* value: {0.789884,0.831468,0.421298,0.50537,0.0375957}
   StMonBind: Failure when applying: Function[Map[Function[If[Less[Slot[1], 0.3], None]], Slot[1]]]
   None *)

Conditional execution of functions

It is natural to want to have the ability to chose a pipeline function application based on a condition.

This can be done with the functions StMonIfElse and StMonWhen.

SeedRandom[34]
StMonUnit[RandomReal[{0, 1}, 5]]⟹
 StMonEchoValue⟹
 StMonIfElse[
  Or @@ (# < 0.4 & /@ #) &,
  (Echo["A too small value is present.", "warning:"]; 
    StMon[Style[#1, Red], #2]) &,
  StMon[Style[#1, Blue], #2] &]⟹
 StMonEchoValue

 (* value: {0.789884,0.831468,0.421298,0.50537,0.0375957}
    warning: A too small value is present.
    value: {0.789884,0.831468,0.421298,0.50537,0.0375957}
    StMon[{0.789884,0.831468,0.421298,0.50537,0.0375957},<||>] *)

Remark: Using flow control functions like StMonIfElse and StMonWhen with appropriate messages is a better way of handling computations that might fail. The silent failures handling of the basic Maybe monad is convenient only in a small number of use cases.

Iterative functions

The last group of pipeline flow control functions we consider comprises iterative functions that provide the functionalities of Nest, NestWhile, FoldList, etc.

In [AA3] these functionalities are provided through the function StMonIterate.

Here is a basic example using Nest that corresponds to Nest[#+1&,1,3]:

StMonUnit[1]⟹StMonIterate[Nest, (StMon[#1 + 1, #2]) &, 3]

(* StMon[4, <||>] *)

Consider this command that uses the full signature of NestWhileList:

NestWhileList[# + 1 &, 1, # < 10 &, 1, 4]

(* {1, 2, 3, 4, 5} *)

Here is the corresponding StMon iteration code:

StMonUnit[1]⟹StMonIterate[NestWhileList, (StMon[#1 + 1, #2]) &, (#[[1]] < 10) &, 1, 4]

(* StMon[{1, 2, 3, 4, 5}, <||>] *)

Here is another results accumulation example with FixedPointList :

StMonUnit[1.]⟹
 StMonIterate[FixedPointList, (StMon[(#1 + 2/#1)/2, #2]) &]

(* StMon[{1., 1.5, 1.41667, 1.41422, 1.41421, 1.41421, 1.41421}, <||>] *)

When the functions NestList, NestWhileList, FixedPointList are used with StMonIterate their results can be stored in the context. Here is an example:

StMonUnit[1.]⟹
 StMonIterate[FixedPointList, (StMon[(#1 + 2/#1)/2, #2]) &, "fpData"]

(* StMon[{1., 1.5, 1.41667, 1.41422, 1.41421, 1.41421, 1.41421}, <|"fpData" -> {StMon[1., <||>], 
    StMon[1.5, <||>], StMon[1.41667, <||>], StMon[1.41422, <||>], StMon[1.41421, <||>], 
    StMon[1.41421, <||>], StMon[1.41421, <||>]} |>] *)

More elaborate tests can be found in [AA8].

Partial pipelines

Because of the associativity law we can design pipeline flows based on functions made of “sub-pipelines.”

fEcho = Function[{x, ct}, StMonUnit[x, ct]⟹StMonEchoValue⟹StMonEchoContext];

fDIter = Function[{x, ct}, 
   StMonUnit[y^x, ct]⟹StMonIterate[FixedPointList, StMonUnit@D[#, y] &, 20]];

StMonUnit[7]⟹fEcho⟹fDIter⟹fEcho;

(*
  value: 7
  context: <||>
  value: {y^7,7 y^6,42 y^5,210 y^4,840 y^3,2520 y^2,5040 y,5040,0,0}
  context: <||> *)

General work-flow of monad code generation utilization

With the abilities to generate and utilize monad codes it is natural to consider the following work flow. (Also shown in the diagram below.)

Come up with an idea that can be expressed with monadic programming.
Look for suitable monad implementation.
If there is no such implementation, make one (or two, or five.)
Having a suitable monad implementation, generate the monad code.
Implement additional pipeline functions addressing envisioned use cases.
Start making pipelines for the problem domain of interest.
Are the pipelines are satisfactory? If not go to 5. (Or 2.)

Monad templates

The template nature of the general monads can be exemplified with the group of functions in the package StateMonadCodeGenerator.m, [4].

They are in five groups:

base monad functions (unit testing, binding),
display of the value and context,
context manipulation (deposit, retrieval, modification),
flow governing (optional new value, conditional function application, iteration),
other convenience functions.

We can say that all monad implementations will have their own versions of these groups of functions. The more specialized monads will have functions specific to their intended use. Such special monads are discussed in the case study sections.

Software design with monadic programming

The application of monadic programming to a particular problem domain is very similar to designing a software framework or designing and implementing a Domain Specific Language (DSL).

The answers of the question “When to use monadic programming?” can form a large list. This section provides only a couple of general, personal viewpoints on monadic programming in software design and architecture. The principles of monadic programming can be used to build systems from scratch (like Haskell and Scala.) Here we discuss making specialized software with or within already existing systems.

Framework design

Software framework design is about architectural solutions that capture the commonality and variability in a problem domain in such a way that: 1) significant speed-up can be achieved when making new applications, and 2) a set of policies can be imposed on the new applications.

The rigidness of the framework provides and supports its flexibility — the framework has a backbone of rigid parts and a set of “hot spots” where new functionalities are plugged-in.

Usually Object-Oriented Programming (OOP) frameworks provide inversion of control — the general work-flow is already established, only parts of it are changed. (This is characterized with “leave the driving to us” and “don’t call us we will call you.”)

The point of utilizing monadic programming is to be able to easily create different new work-flows that share certain features. (The end user is the driver, on certain rail paths.)

In my opinion making a software framework of small to moderate size with monadic programming principles would produce a library of functions each with polymorphic behaviour that can be easily sequenced in monadic pipelines. This can be contrasted with OOP framework design in which we are more likely to end up with backbone structures that (i) are static and tree-like, and (ii) are extended or specialized by plugging-in relevant objects. (Those plugged-in objects themselves can be trees, but hopefully short ones.)

DSL development

Given a problem domain the general monad structure can be used to shape and guide the development of DSLs for that problem domain.

Generally, in order to make a DSL we have to choose the language syntax and grammar. Using monadic programming the syntax and grammar commands are clear. (The monad pipelines are the commands.) What is left is “just” the choice of particular functions and their implementations.

Another way to develop such a DSL is through a grammar of natural language commands. Generally speaking, just designing the grammar — without developing the corresponding interpreters — would be very helpful in figuring out the components at play. Monadic programming meshes very well with this approach and applying the two approaches together can be very fruitful.

Contextual monad classification (case study)

In this section we show an extension of the State monad into a monad aimed at machine learning classification work-flows.

Motivation

We want to provide a DSL for doing machine learning classification tasks that allows us:

to do basic summarization and visualization of the data,
to control splitting of the data into training and testing sets;
to apply the built-in classifiers;
to apply classifier ensembles (see [AA9] and [AA10]);
to evaluate classifier performances with standard measures and
ROC plots.

Also, we want the DSL design to provide clear directions how to add (hook-up or plug-in) new functionalities.

The package [AA4] discussed below provides such a DSL through monadic programming.

Package and data loading

This loads the package [AA4]:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicContextualClassification.m"]

This gets some test data (the Titanic dataset):

dataName = "Titanic";
ds = Dataset[Flatten@*List @@@ ExampleData[{"MachineLearning", dataName}, "Data"]];
varNames = Flatten[List @@ ExampleData[{"MachineLearning", dataName}, "VariableDescriptions"]];
varNames = StringReplace[varNames, "passenger" ~~ (WhitespaceCharacter ..) -> ""];
If[dataName == "FisherIris", varNames = Most[varNames]];
ds = ds[All, AssociationThread[varNames -> #] &];

Monad design

The package [AA4] provides functions for the monad ClCon — the functions implemented in [AA4] have the prefix “ClCon”.

The classifier contexts are Association objects. The pipeline values can have the form:

ClCon[ val, context:(_String|_Association) ]

The ClCon specific monad functions deposit or retrieve values from the context with the keys: “trainData”, “testData”, “classifier”. The general idea is that if the current value of the pipeline cannot provide all arguments for a ClCon function, then the needed arguments are taken from the context. If that fails, then an message is issued. This is illustrated with the following pipeline with comments example.

The pipeline and results above demonstrate polymorphic behaviour over the classifier variable in the context: different functions are used if that variable is a ClassifierFunction object or an association of named ClassifierFunction objects.

Note the demonstrated granularity and sequentiality of the operations coming from using a monad structure. With those kind of operations it would be easy to make interpreters for natural language DSLs.

Another usage example

This monadic pipeline in this example goes through several stages: data summary, classifier training, evaluation, acceptance test, and if the results are rejected a new classifier is made with a different algorithm using the same data splitting. The context keeps track of the data and its splitting. That allows the conditional classifier switch to be concisely specified.

First let us define a function that takes a Classify method as an argument and makes a classifier and calculates performance measures.

ClSubPipe[method_String] :=
  Function[{x, ct},
   ClConUnit[x, ct]⟹
    ClConMakeClassifier[method]⟹
    ClConEchoFunctionContext["classifier:", 
     ClassifierInformation[#["classifier"], Method] &]⟹
    ClConEchoFunctionContext["training time:", ClassifierInformation[#["classifier"], "TrainingTime"] &]⟹
    ClConClassifierMeasurements[{"Accuracy", "Precision", "Recall"}]⟹
    ClConEchoValue⟹
    ClConEchoFunctionContext[
     ClassifierMeasurements[#["classifier"], 
     ClConToNormalClassifierData[#["testData"]], "ROCCurve"] &]
   ];

Using the sub-pipeline function ClSubPipe we make the outlined pipeline.

SeedRandom[12]
res =
  ClConUnit[ds]⟹
   ClConSplitData[0.7]⟹
   ClConEchoFunctionValue["summaries:", ColumnForm[Normal[RecordsSummary /@ #]] &]⟹
   ClConEchoFunctionValue["xtabs:", 
    MatrixForm[CrossTensorate[Count == varNames[[1]] + varNames[[-1]], #]] & /@ # &]⟹
   ClSubPipe["LogisticRegression"]⟹
   (If[#1["Accuracy"] > 0.8,
      Echo["Good accuracy!", "Success:"]; ClConFail,
      Echo["Make a new classifier", "Inaccurate:"]; 
      ClConUnit[#1, #2]] &)⟹
   ClSubPipe["RandomForest"];

Tracing monad pipelines (case study)

The monadic implementations in the package MonadicTracing.m, [AA5] allow tracking of the pipeline execution of functions within other monads.

The primary reason for developing the package was the desire to have the ability to print a tabulated trace of code and comments using the usual monad pipeline notation. (I.e. without conversion to strings etc.)

It turned out that by programming MonadicTracing.m I came up with a monad transformer; see [Wk2], [H2].

Package loading

This loads the package [AA5]:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicTracing.m"]

Usage example

This generates a Maybe monad to be used in the example (for the prefix “Perhaps”):

GenerateMaybeMonadCode["Perhaps"]
GenerateMaybeMonadSpecialCode["Perhaps"]

In following example we can see that pipeline functions of the Perhaps monad are interleaved with comment strings. Producing the grid of functions and comments happens “naturally” with the monad function TraceMonadEchoGrid.

data = RandomInteger[10, 15];

TraceMonadUnit[PerhapsUnit[data]]⟹"lift to monad"⟹
  TraceMonadEchoContext⟹
  PerhapsFilter[# > 3 &]⟹"filter current value"⟹
  PerhapsEcho⟹"display current value"⟹
  PerhapsWhen[#[[3]] > 3 &, 
   PerhapsEchoFunction[Style[#, Red] &]]⟹
  (Perhaps[#/4] &)⟹
  PerhapsEcho⟹"display current value again"⟹
  TraceMonadEchoGrid[Grid[#, Alignment -> Left] &];

Note that :

the tracing is initiated by just using TraceMonadUnit;
pipeline functions (actual code) and comments are interleaved;
putting a comment string after a pipeline function is optional.

Another example is the ClCon pipeline in the sub-section “Monad design” in the previous section.

Summary

This document presents a style of using monadic programming in Wolfram Language (Mathematica). The style has some shortcomings, but it definitely provides convenient features for day-to-day programming and in coming up with architectural designs.

The style is based on WL’s basic language features. As a consequence it is fairly concise and produces light overhead.

Ideally, the packages for the code generation of the basic Maybe and State monads would serve as starting points for other more general or more specialized monadic programs.

References

Monadic programming

[Wk1] Wikipedia entry: Monad (functional programming), URL: https://en.wikipedia.org/wiki/Monad_(functional_programming) .

[Wk2] Wikipedia entry: Monad transformer, URL: https://en.wikipedia.org/wiki/Monad_transformer .

[Wk3] Wikipedia entry: Software Design Pattern, URL: https://en.wikipedia.org/wiki/Software_design_pattern .

[H1] Haskell.org article: Monad laws, URL: https://wiki.haskell.org/Monad_laws.

[H2] Sheng Liang, Paul Hudak, Mark Jones, “Monad transformers and modular interpreters”, (1995), Proceedings of the 22nd ACM SIGPLAN-SIGACT symposium on Principles of programming languages. New York, NY: ACM. pp. 333[Dash]343. doi:10.1145/199448.199528.

[H3] Philip Wadler, “The essence of functional programming”, (1992), 19’th Annual Symposium on Principles of Programming Languages, Albuquerque, New Mexico, January 1992.

R

[R1] Hadley Wickham et al., dplyr: A Grammar of Data Manipulation, (2014), tidyverse at GitHub, URL: https://github.com/tidyverse/dplyr . (See also, http://dplyr.tidyverse.org .)

Mathematica / Wolfram Language

[WL1] Leonid Shifrin, “Metaprogramming in Wolfram Language”, (2012), Mathematica StackExchange. (Also posted at Wolfram Community in 2017.) URL of the Mathematica StackExchange answer: https://mathematica.stackexchange.com/a/2352/34008 . URL of the Wolfram Community post: http://community.wolfram.com/groups/-/m/t/1121273 .

MathematicaForPrediction

[AA1] Anton Antonov, “Implementation of Object-Oriented Programming Design Patterns in Mathematica”, (2016) MathematicaForPrediction at GitHub, https://github.com/antononcube/MathematicaForPrediction.

[AA2] Anton Antonov, Maybe monad code generator Mathematica package, (2017), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/MonadicProgramming/MaybeMonadCodeGenerator.m .

[AA3] Anton Antonov, State monad code generator Mathematica package, (2017), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/MonadicProgramming/StateMonadCodeGenerator.m .

[AA4] Anton Antonov, Monadic contextual classification Mathematica package, (2017), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/MonadicProgramming/MonadicContextualClassification.m .

[AA5] Anton Antonov, Monadic tracing Mathematica package, (2017), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/MonadicProgramming/MonadicTracing.m .

[AA6] Anton Antonov, MathematicaForPrediction utilities, (2014), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/MathematicaForPredictionUtilities.m .

[AA7] Anton Antonov, Simple monadic programming, (2017), MathematicaForPrediction at GitHub. (Preliminary version, 40% done.) URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/Documentation/Simple-monadic-programming.pdf .

[AA8] Anton Antonov, Generated State Monad Mathematica unit tests, (2017), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/UnitTests/GeneratedStateMonadTests.m .

[AA9] Anton Antonov, Classifier ensembles functions Mathematica package, (2016), MathematicaForPrediction at GitHub. URL: https://github.com/antononcube/MathematicaForPrediction/blob/master/ClassifierEnsembles.m .

[AA10] Anton Antonov, “ROC for classifier ensembles, bootstrapping, damaging, and interpolation”, (2016), MathematicaForPrediction at WordPress. URL: https://mathematicaforprediction.wordpress.com/2016/10/15/roc-for-classifier-ensembles-bootstrapping-damaging-and-interpolation/ .

Text analysis of Trump tweets

Posted on November 21, 2016 by Anton Antonov Antonov

Introduction

This post is to proclaim the MathematicaVsR at GitHub project “Text analysis of Trump tweets” in which we compare Mathematica and R over text analyses of Twitter messages made by Donald Trump (and his staff) before the USA president elections in 2016.

The project follows and extends the exposition and analysis of the R-based blog post "Text analysis of Trump’s tweets confirms he writes only the (angrier) Android half" by David Robinson at VarianceExplained.org; see [1].

The blog post [1] links to several sources that claim that during the election campaign Donald Trump tweeted from his Android phone and his campaign staff tweeted from an iPhone. The blog post [1] examines this hypothesis in a quantitative way (using various R packages.)

The hypothesis in question is well summarized with the tweet:

Every non-hyperbolic tweet is from iPhone (his staff).
Every hyperbolic tweet is from Android (from him). pic.twitter.com/GWr6D8h5ed
— Todd Vaziri (@tvaziri) August 6, 2016

This conjecture is fairly well supported by the following mosaic plots, [2]:

We can see the that Twitter messages from iPhone are much more likely to be neutral, and the ones from Android are much more polarized. As Christian Rudder (one of the founders of OkCupid, a dating website) explains in the chapter "Death by a Thousand Mehs" of the book "Dataclysm", [3], having a polarizing image (online persona) is a very good strategy to engage online audience:

[…] And the effect isn’t small — being highly polarizing will in fact get you about 70 percent more messages. That means variance allows you to effectively jump several "leagues" up in the dating pecking order — […]

(The mosaic plots above were made for the Mathematica-part of this project. Mosaic plots and weekday tags are not used in [1].)

Concrete steps

The Mathematica-part of this project does not follow closely the blog post [1]. After the ingestion of the data provided in [1], the Mathematica-part applies alternative algorithms to support and extend the analysis in [1].

The sections in the R-part notebook correspond to some — not all — of the sections in the Mathematica-part.

The following list of steps is for the Mathematica-part.

Data ingestion
- The blog post [1] shows how to do in R the ingestion of Twitter data of Donald Trump messages.
- That can be done in Mathematica too using the built-in function ServiceConnect, but that is not necessary since [1] provides a link to the ingested data used [1]:
  load(url("http://varianceexplained.org/files/trump_tweets_df.rda"))
- Which leads to the ingesting of an R data frame in the Mathematica-part using RLink.
Adding tags
- We have to extract device tags for the messages — each message is associated with one of the tags "Android", "iPad", or "iPhone".
- Using the message time-stamps each message is associated with time tags corresponding to the creation time month, hour, weekday, etc.
- Here is summary of the data at this stage:
Time series and time related distributions
- We can make several types of time series plots for general insight and to support the main conjecture.
- Here is a Mathematica made plot for the same statistic computed in [1] that shows differences in tweet posting behavior:
- Here are distributions plots of tweets per weekday:
Classification into sentiments and Facebook topics
- Using the built-in classifiers of Mathematica each tweet message is associated with a sentiment tag and a Facebook topic tag.
- In [1] the results of this step are derived in several stages.
- Here is a mosaic plot for conditional probabilities of devices, topics, and sentiments:
Device-word association rules
- Using Association rule learning device tags are associated with words in the tweets.
- In the Mathematica-part these associations rules are not needed for the sentiment analysis (because of the built-in classifiers.)
- The association rule mining is done mostly to support and extend the text analysis in [1] and, of course, for comparison purposes.
- Here is an example of derived association rules together with their most important measures:

In [1] the sentiments are derived from computed device-word associations, so in [1] the order of steps is 1-2-3-5-4. In Mathematica we do not need the steps 3 and 5 in order to get the sentiments in the 4th step.

Comparison

Using Mathematica for sentiment analysis is much more direct because of the built-in classifiers.

The R-based blog post [1] uses heavily the "pipeline" operator %>% which is kind of a recent addition to R (and it is both fashionable and convenient to use it.) In Mathematica the related operators are Postfix (//), Prefix (@), Infix (~~), Composition (@*), and RightComposition (/*).

Making the time series plots with the R package "ggplot2" requires making special data frames. I am inclined to think that the Mathematica plotting of time series is more direct, but for this task the data wrangling codes in Mathematica and R are fairly comparable.

Generally speaking, the R package "arules" — used in this project for Associations rule learning — is somewhat awkward to use:

it is data frame centric, does not work directly with lists of lists, and
requires the use of factors.

The Apriori implementation in “arules” is much faster than the one in “AprioriAlgorithm.m” — “arules” uses a more efficient algorithm implemented in C.

References

[1] David Robinson, "Text analysis of Trump’s tweets confirms he writes only the (angrier) Android half", (2016), VarianceExplained.org.

[2] Anton Antonov, "Mosaic plots for data visualization", (2014), MathematicaForPrediction at WordPress.

[3] Christian Rudder, Dataclysm, Crown, 2014. ASIN: B00J1IQUX8 .

	Notebook transformat… on LLM помогает в обработке перво…
	Heatmap plots over L… on Extracting Russian casualties…
	Generalized Lanchest… on A monad for Epidemiologic Comp…
	Anton Antonov Antono… on AI vision via Wolfram Lan…
	Anton Antonov Antono… on Nightcore “Conflict…

References

Articles

Mathematica packages and repository functions

Python packages

R packages

Introduction

The overall process

Data

The Apple data

The New York Times data

The search engines

Structure

Implementation

Examples

Apple data search engine examples

Nice, France vs Florida, USA

Italy and Balkan countries driving

The New York Times data search engine examples

References

Data

Articles

Packages, repositories

Version 0.8

Introduction

Contents description

Package load

Data load

Read data

Data summaries

Transform data

Geo-visualizations

Design considerations

The big picture

Large-scale modeling

Flow chart

Two models in the monad

Single-site model workflow

Multi-site model workflow

Single-site models

SEI2HR model

Verbal description

Equations

Single-site model workflow demo

Multi-site workflow demo

Batch simulations and calibration processes

Definitions

Roles

Process

Batch simulation vs calibration

Batch simulations workflow

Model (object) for batch simulations

Direct specification of combinations of parameters

All populations

Focus population

Outer product of parameters

Calibration workflow

Calibration steps

USA COVID-19 data

Calibration targets

Model creation

Calibration

Using different minimization methods and distance functions

Verification of the fit

Conclusions from the calibration results

Future plans

More unit tests and random unit tests

More comprehensive calibration guides and documentation

Full correspondence between the Mathematica and R implementations

Model transfer between Mathematica and R

Conversational agent

Different target languages

References

Articles

Repositories, packages

Screenshots

References

Coronavirus

Modeling

R code/software

References